Objection-Based Causal Networks

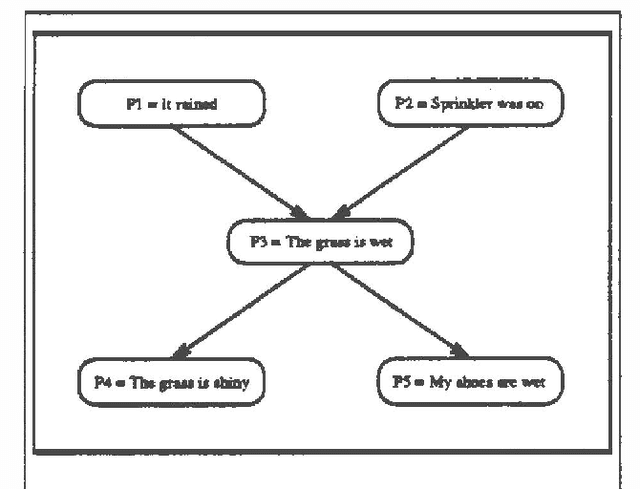
This paper introduces the notion of objection-based causal networks which resemble probabilistic causal networks except that they are quantified using objections. An objection is a logical sentence and denotes a condition under which a, causal dependency does not exist. Objection-based causal networks enjoy almost all the properties that make probabilistic causal networks popular, with the added advantage that objections are, arguably more intuitive than probabilities.

Argument Calculus and Networks

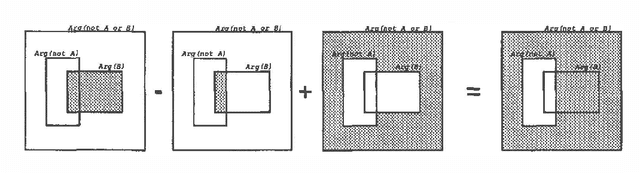
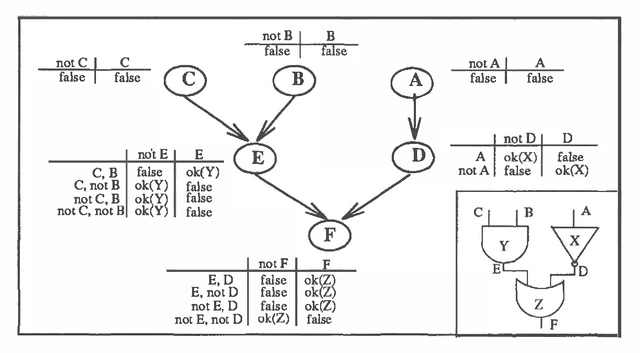
A major reason behind the success of probability calculus is that it possesses a number of valuable tools, which are based on the notion of probabilistic independence. In this paper, I identify a notion of logical independence that makes some of these tools available to a class of propositional databases, called argument databases. Specifically, I suggest a graphical representation of argument databases, called argument networks, which resemble Bayesian networks. I also suggest an algorithm for reasoning with argument networks, which resembles a basic algorithm for reasoning with Bayesian networks. Finally, I show that argument networks have several applications: Nonmonotonic reasoning, truth maintenance, and diagnosis.

On the Relation between Kappa Calculus and Probabilistic Reasoning

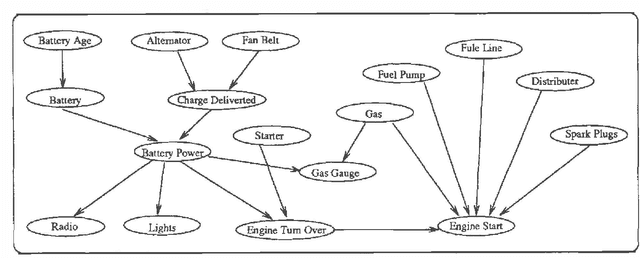
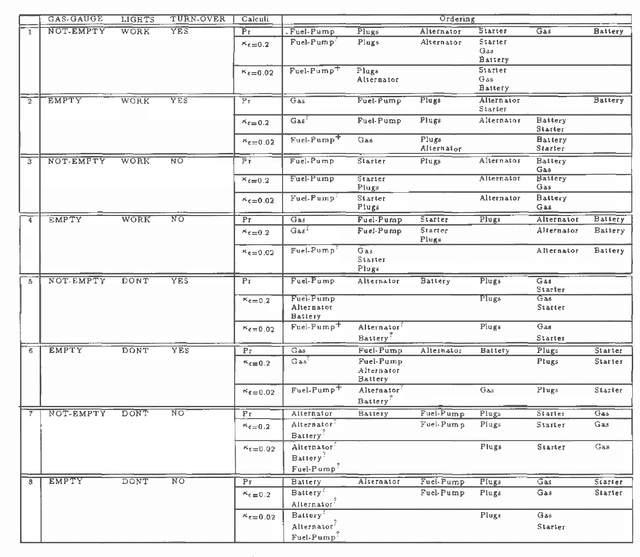
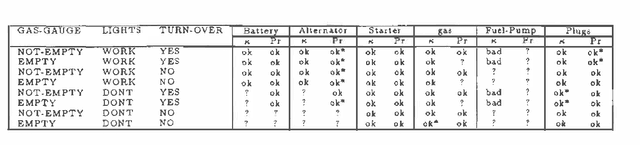
We study the connection between kappa calculus and probabilistic reasoning in diagnosis applications. Specifically, we abstract a probabilistic belief network for diagnosing faults into a kappa network and compare the ordering of faults computed using both methods. We show that, at least for the example examined, the ordering of faults coincide as long as all the causal relations in the original probabilistic network are taken into account. We also provide a formal analysis of some network structures where the two methods will differ. Both kappa rankings and infinitesimal probabilities have been used extensively to study default reasoning and belief revision. But little has been done on utilizing their connection as outlined above. This is partly because the relation between kappa and probability calculi assumes that probabilities are arbitrarily close to one (or zero). The experiments in this paper investigate this relation when this assumption is not satisfied. The reported results have important implications on the use of kappa rankings to enhance the knowledge engineering of uncertainty models.

Action Networks: A Framework for Reasoning about Actions and Change under Uncertainty

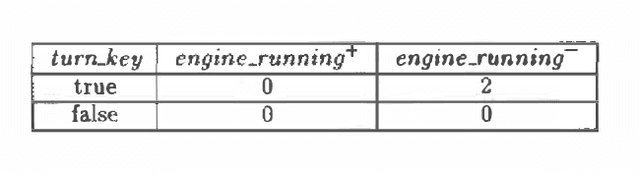
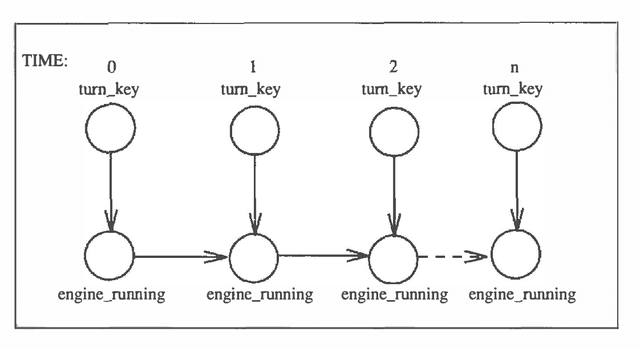
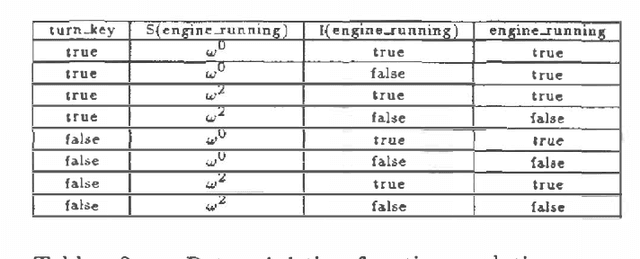
This work proposes action networks as a semantically well-founded framework for reasoning about actions and change under uncertainty. Action networks add two primitives to probabilistic causal networks: controllable variables and persistent variables. Controllable variables allow the representation of actions as directly setting the value of specific events in the domain, subject to preconditions. Persistent variables provide a canonical model of persistence according to which both the state of a variable and the causal mechanism dictating its value persist over time unless intervened upon by an action (or its consequences). Action networks also allow different methods for quantifying the uncertainty in causal relationships, which go beyond traditional probabilistic quantification. This paper describes both recent results and work in progress.

Conditioning Methods for Exact and Approximate Inference in Causal Networks

We present two algorithms for exact and approximate inference in causal networks. The first algorithm, dynamic conditioning, is a refinement of cutset conditioning that has linear complexity on some networks for which cutset conditioning is exponential. The second algorithm, B-conditioning, is an algorithm for approximate inference that allows one to trade-off the quality of approximations with the computation time. We also present some experimental results illustrating the properties of the proposed algorithms.

A Standard Approach for Optimizing Belief Network Inference using Query DAGs

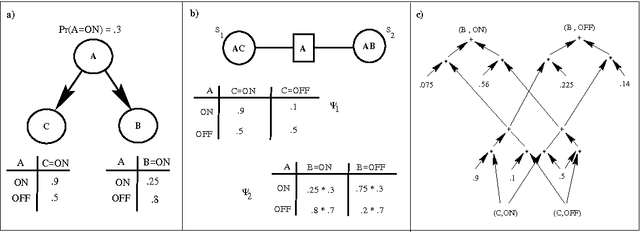
This paper proposes a novel, algorithm-independent approach to optimizing belief network inference. rather than designing optimizations on an algorithm by algorithm basis, we argue that one should use an unoptimized algorithm to generate a Q-DAG, a compiled graphical representation of the belief network, and then optimize the Q-DAG and its evaluator instead. We present a set of Q-DAG optimizations that supplant optimizations designed for traditional inference algorithms, including zero compression, network pruning and caching. We show that our Q-DAG optimizations require time linear in the Q-DAG size, and significantly simplify the process of designing algorithms for optimizing belief network inference.

Dynamic Jointrees

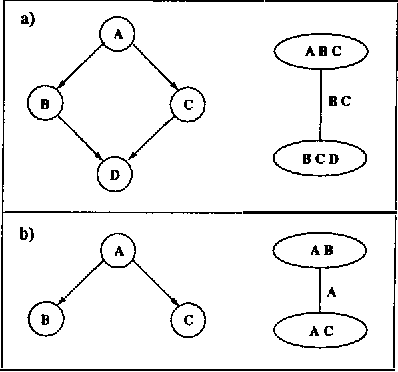
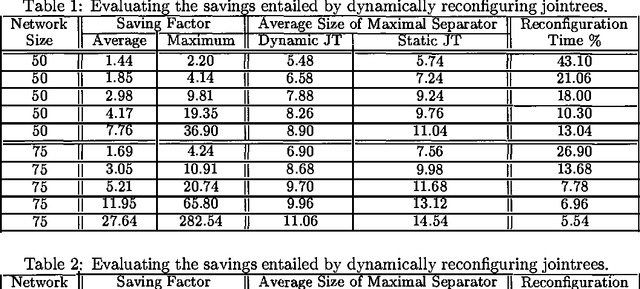
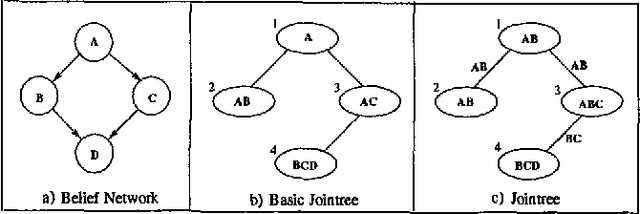
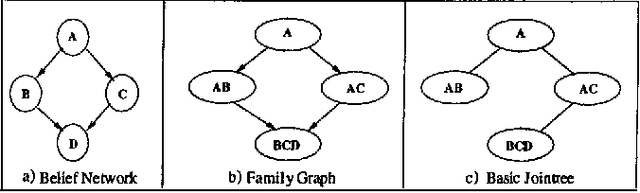
It is well known that one can ignore parts of a belief network when computing answers to certain probabilistic queries. It is also well known that the ignorable parts (if any) depend on the specific query of interest and, therefore, may change as the query changes. Algorithms based on jointrees, however, do not seem to take computational advantage of these facts given that they typically construct jointrees for worst-case queries; that is, queries for which every part of the belief network is considered relevant. To address this limitation, we propose in this paper a method for reconfiguring jointrees dynamically as the query changes. The reconfiguration process aims at maintaining a jointree which corresponds to the underlying belief network after it has been pruned given the current query. Our reconfiguration method is marked by three characteristics: (a) it is based on a non-classical definition of jointrees; (b) it is relatively efficient; and (c) it can reuse some of the computations performed before a jointree is reconfigured. We present preliminary experimental results which demonstrate significant savings over using static jointrees when query changes are considerable.

Any-Space Probabilistic Inference

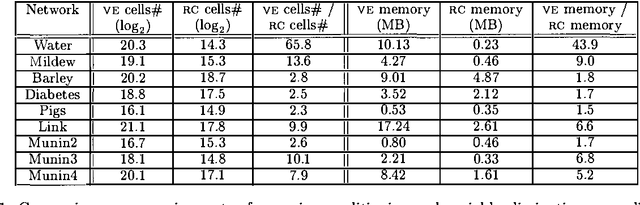
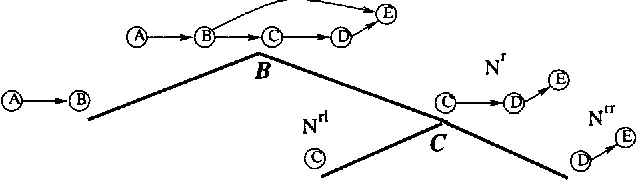
We have recently introduced an any-space algorithm for exact inference in Bayesian networks, called Recursive Conditioning, RC, which allows one to trade space with time at increments of X-bytes, where X is the number of bytes needed to cache a floating point number. In this paper, we present three key extensions of RC. First, we modify the algorithm so it applies to more general factorization of probability distributions, including (but not limited to) Bayesian network factorizations. Second, we present a forgetting mechanism which reduces the space requirements of RC considerably and then compare such requirmenets with those of variable elimination on a number of realistic networks, showing orders of magnitude improvements in certain cases. Third, we present a version of RC for computing maximum a posteriori hypotheses (MAP), which turns out to be the first MAP algorithm allowing a smooth time-space tradeoff. A key advantage of presented MAP algorithm is that it does not have to start from scratch each time a new query is presented, but can reuse some of its computations across multiple queries, leading to significant savings in ceratain cases.

A Differential Approach to Inference in Bayesian Networks

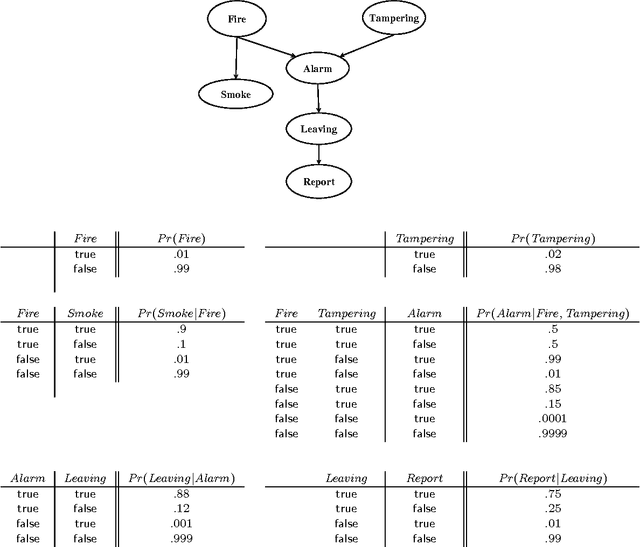
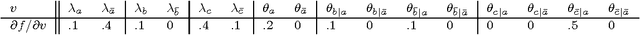
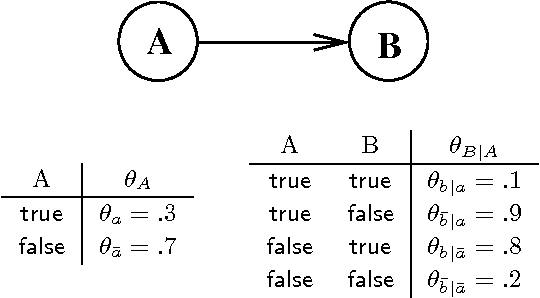
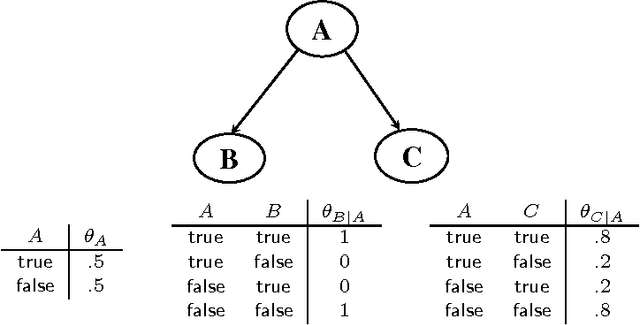
We present a new approach for inference in Bayesian networks, which is mainly based on partial differentiation. According to this approach, one compiles a Bayesian network into a multivariate polynomial and then computes the partial derivatives of this polynomial with respect to each variable. We show that once such derivatives are made available, one can compute in constant-time answers to a large class of probabilistic queries, which are central to classical inference, parameter estimation, model validation and sensitivity analysis. We present a number of complexity results relating to the compilation of such polynomials and to the computation of their partial derivatives. We argue that the combined simplicity, comprehensiveness and computational complexity of the presented framework is unique among existing frameworks for inference in Bayesian networks.

Approximating MAP using Local Search

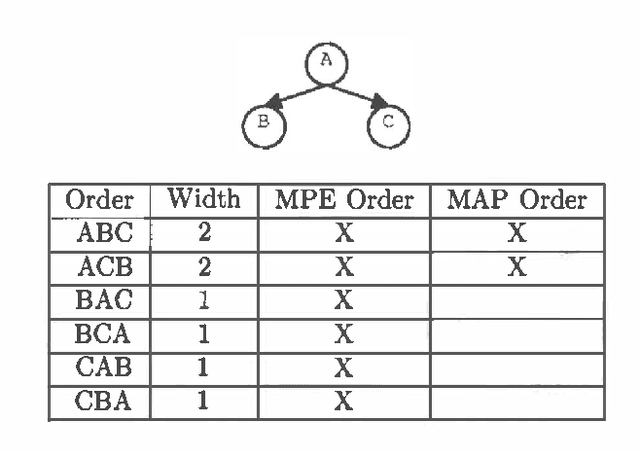
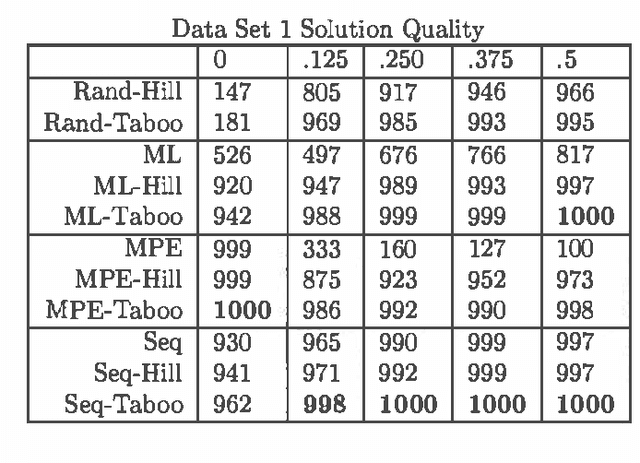
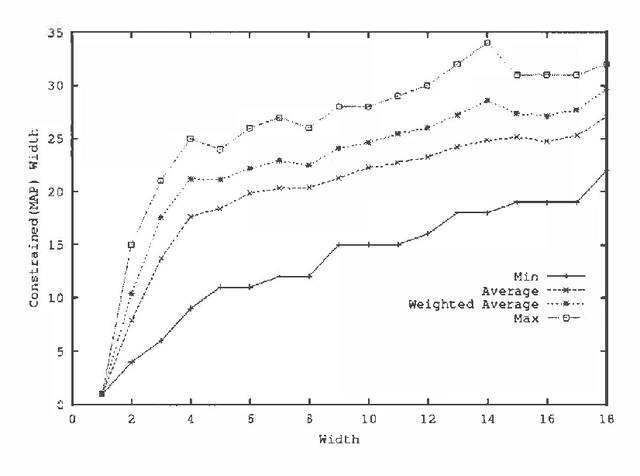
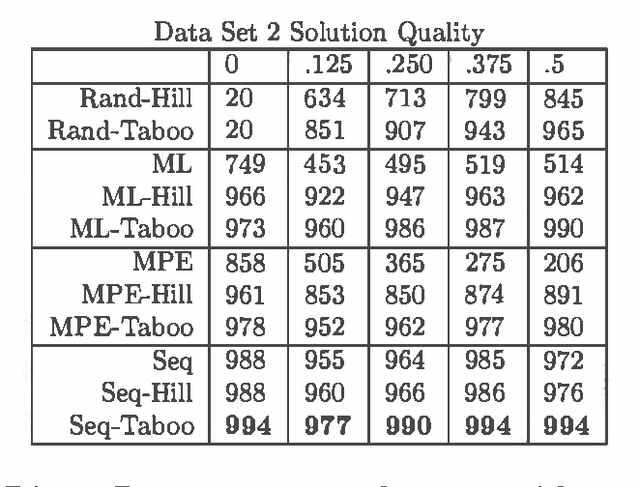
MAP is the problem of finding a most probable instantiation of a set of variables in a Bayesian network, given evidence. Unlike computing marginals, posteriors, and MPE (a special case of MAP), the time and space complexity of MAP is not only exponential in the network treewidth, but also in a larger parameter known as the "constrained" treewidth. In practice, this means that computing MAP can be orders of magnitude more expensive than computingposteriors or MPE. Thus, practitioners generally avoid MAP computations, resorting instead to approximating them by the most likely value for each MAP variableseparately, or by MPE.We present a method for approximating MAP using local search. This method has space complexity which is exponential onlyin the treewidth, as is the complexity of each search step. We investigate the effectiveness of different local searchmethods and several initialization strategies and compare them to otherapproximation schemes.Experimental results show that local search provides a much more accurate approximation of MAP, while requiring few search steps.Practically, this means that the complexity of local search is often exponential only in treewidth as opposed to the constrained treewidth, making approximating MAP as efficient as other computations.