Statistically guided deep learning

We present a theoretically well-founded deep learning algorithm for nonparametric regression. It uses over-parametrized deep neural networks with logistic activation function, which are fitted to the given data via gradient descent. We propose a special topology of these networks, a special random initialization of the weights, and a data-dependent choice of the learning rate and the number of gradient descent steps. We prove a theoretical bound on the expected $L_2$ error of this estimate, and illustrate its finite sample size performance by applying it to simulated data. Our results show that a theoretical analysis of deep learning which takes into account simultaneously optimization, generalization and approximation can result in a new deep learning estimate which has an improved finite sample performance.

Analysis of the rate of convergence of an over-parametrized convolutional neural network image classifier learned by gradient descent

Image classification based on over-parametrized convolutional neural networks with a global average-pooling layer is considered. The weights of the network are learned by gradient descent. A bound on the rate of convergence of the difference between the misclassification risk of the newly introduced convolutional neural network estimate and the minimal possible value is derived.

On the rate of convergence of an over-parametrized Transformer classifier learned by gradient descent

One of the most recent and fascinating breakthroughs in artificial intelligence is ChatGPT, a chatbot which can simulate human conversation. ChatGPT is an instance of GPT4, which is a language model based on generative gredictive gransformers. So if one wants to study from a theoretical point of view, how powerful such artificial intelligence can be, one approach is to consider transformer networks and to study which problems one can solve with these networks theoretically. Here it is not only important what kind of models these network can approximate, or how they can generalize their knowledge learned by choosing the best possible approximation to a concrete data set, but also how well optimization of such transformer network based on concrete data set works. In this article we consider all these three different aspects simultaneously and show a theoretical upper bound on the missclassification probability of a transformer network fitted to the observed data. For simplicity we focus in this context on transformer encoder networks which can be applied to define an estimate in the context of a classification problem involving natural language.

On the rate of convergence of a deep recurrent neural network estimate in a regression problem with dependent data

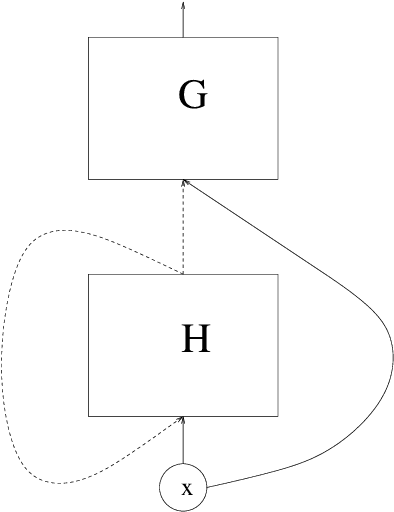
A regression problem with dependent data is considered. Regularity assumptions on the dependency of the data are introduced, and it is shown that under suitable structural assumptions on the regression function a deep recurrent neural network estimate is able to circumvent the curse of dimensionality.

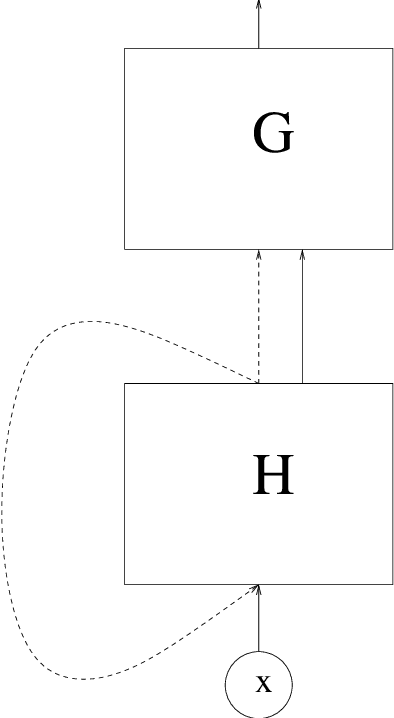
Deep Learning and MARS: A Connection

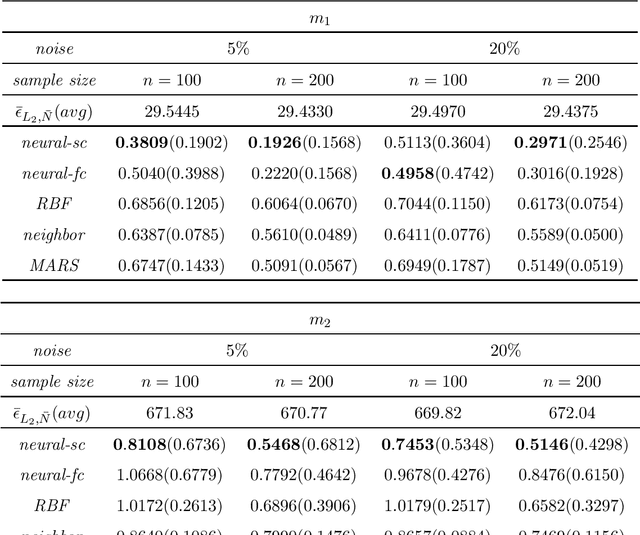
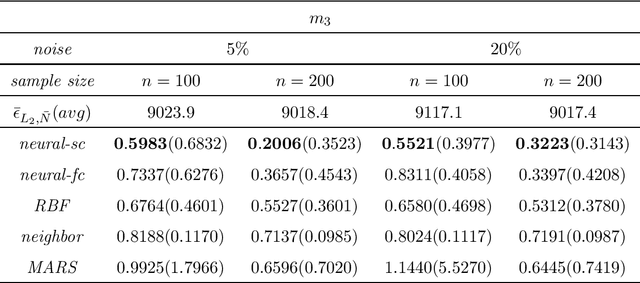
We consider least squares regression estimates using deep neural networks. We show that these estimates satisfy an oracle inequality, which implies that (up to a logarithmic factor) the error of these estimates is at least as small as the optimal possible error bound which one would expect for MARS in case that this procedure would work in the optimal way. As a result we show that our neural networks are able to achieve a dimensionality reduction in case that the regression function locally has low dimensionality. This assumption seems to be realistic in real-world applications, since selected high-dimensional data are often confined to locally-low-dimensional distributions. In our simulation study we provide numerical experiments to support our theoretical results and to compare our estimate with other conventional nonparametric regression estimates, especially with MARS. The use of our estimates is illustrated through a real data analysis.