Concealment of Intent: A Game-Theoretic Analysis

As large language models (LLMs) grow more capable, concerns about their safe deployment have also grown. Although alignment mechanisms have been introduced to deter misuse, they remain vulnerable to carefully designed adversarial prompts. In this work, we present a scalable attack strategy: intent-hiding adversarial prompting, which conceals malicious intent through the composition of skills. We develop a game-theoretic framework to model the interaction between such attacks and defense systems that apply both prompt and response filtering. Our analysis identifies equilibrium points and reveals structural advantages for the attacker. To counter these threats, we propose and analyze a defense mechanism tailored to intent-hiding attacks. Empirically, we validate the attack's effectiveness on multiple real-world LLMs across a range of malicious behaviors, demonstrating clear advantages over existing adversarial prompting techniques.

DART: aDaptive Accept RejecT for non-linear top-K subset identification

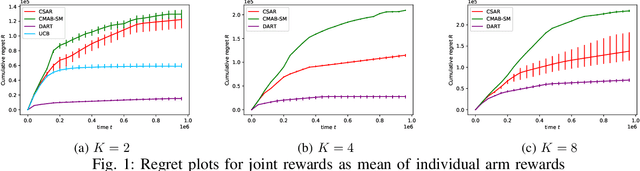
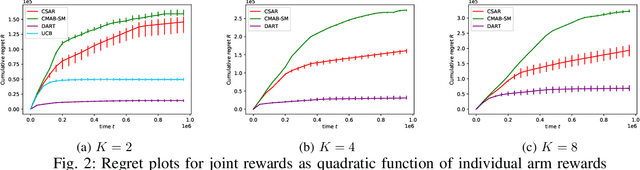
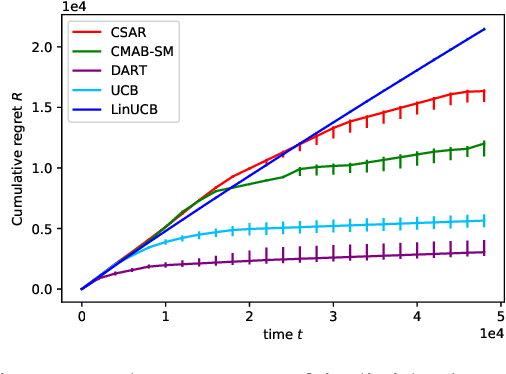
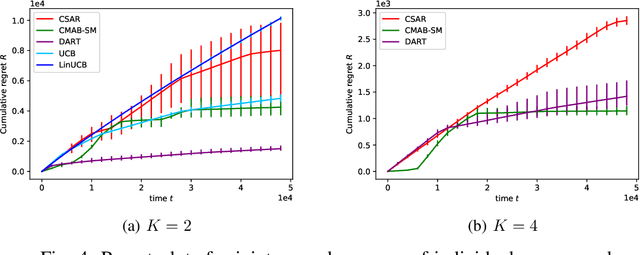
We consider the bandit problem of selecting $K$ out of $N$ arms at each time step. The reward can be a non-linear function of the rewards of the selected individual arms. The direct use of a multi-armed bandit algorithm requires choosing among $\binom{N}{K}$ options, making the action space large. To simplify the problem, existing works on combinatorial bandits {typically} assume feedback as a linear function of individual rewards. In this paper, we prove the lower bound for top-$K$ subset selection with bandit feedback with possibly correlated rewards. We present a novel algorithm for the combinatorial setting without using individual arm feedback or requiring linearity of the reward function. Additionally, our algorithm works on correlated rewards of individual arms. Our algorithm, aDaptive Accept RejecT (DART), sequentially finds good arms and eliminates bad arms based on confidence bounds. DART is computationally efficient and uses storage linear in $N$. Further, DART achieves a regret bound of $\tilde{\mathcal{O}}(K\sqrt{KNT})$ for a time horizon $T$, which matches the lower bound in bandit feedback up to a factor of $\sqrt{\log{2NT}}$. When applied to the problem of cross-selling optimization and maximizing the mean of individual rewards, the performance of the proposed algorithm surpasses that of state-of-the-art algorithms. We also show that DART significantly outperforms existing methods for both linear and non-linear joint reward environments.