DO-EM: Density Operator Expectation Maximization

Density operators, quantum generalizations of probability distributions, are gaining prominence in machine learning due to their foundational role in quantum computing. Generative modeling based on density operator models (\textbf{DOMs}) is an emerging field, but existing training algorithms -- such as those for the Quantum Boltzmann Machine -- do not scale to real-world data, such as the MNIST dataset. The Expectation-Maximization algorithm has played a fundamental role in enabling scalable training of probabilistic latent variable models on real-world datasets. \textit{In this paper, we develop an Expectation-Maximization framework to learn latent variable models defined through \textbf{DOMs} on classical hardware, with resources comparable to those used for probabilistic models, while scaling to real-world data.} However, designing such an algorithm is nontrivial due to the absence of a well-defined quantum analogue to conditional probability, which complicates the Expectation step. To overcome this, we reformulate the Expectation step as a quantum information projection (QIP) problem and show that the Petz Recovery Map provides a solution under sufficient conditions. Using this formulation, we introduce the Density Operator Expectation Maximization (DO-EM) algorithm -- an iterative Minorant-Maximization procedure that optimizes a quantum evidence lower bound. We show that the \textbf{DO-EM} algorithm ensures non-decreasing log-likelihood across iterations for a broad class of models. Finally, we present Quantum Interleaved Deep Boltzmann Machines (\textbf{QiDBMs}), a \textbf{DOM} that can be trained with the same resources as a DBM. When trained with \textbf{DO-EM} under Contrastive Divergence, a \textbf{QiDBM} outperforms larger classical DBMs in image generation on the MNIST dataset, achieving a 40--60\% reduction in the Fr\'echet Inception Distance.

Reliable quantum kernel classification using fewer circuit evaluations

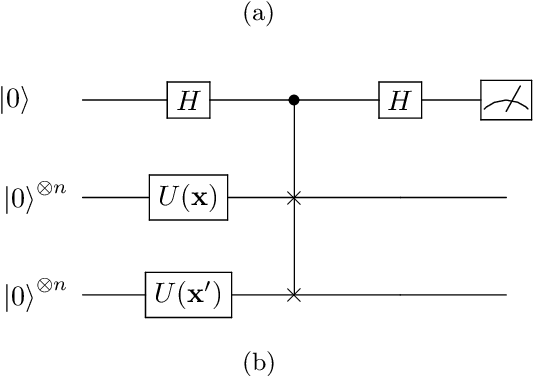
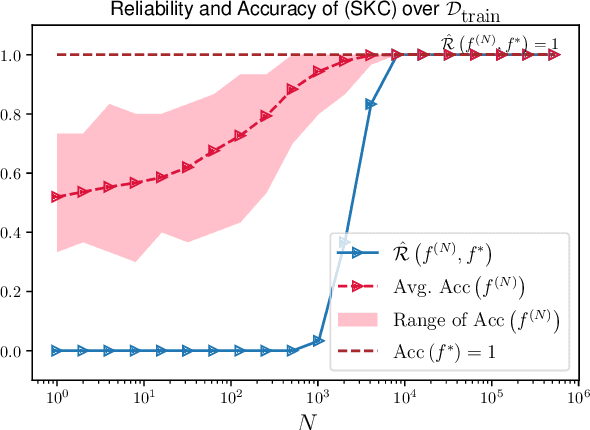
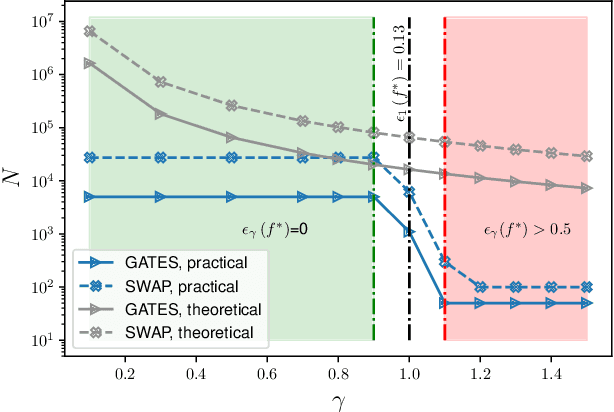
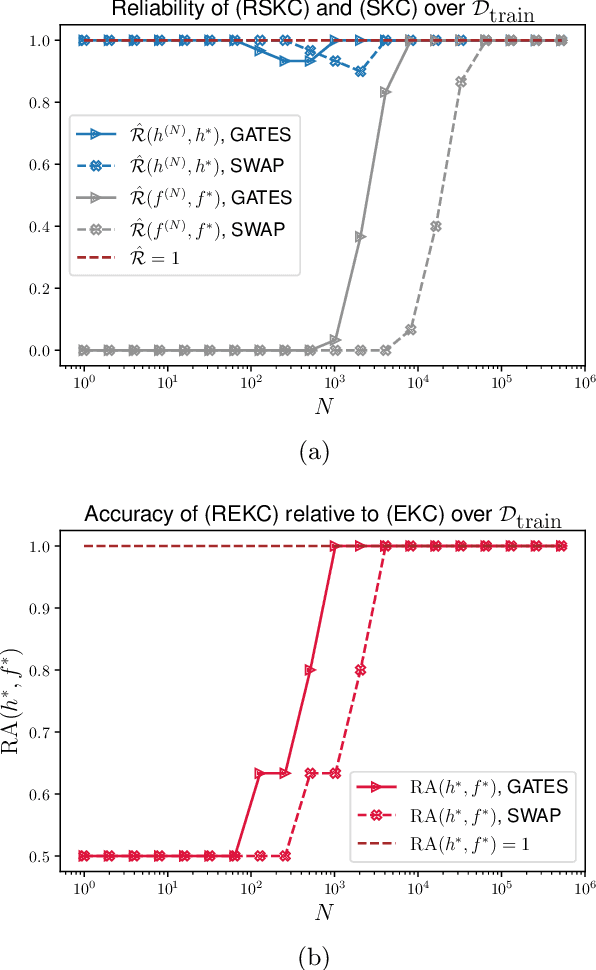
Quantum kernel methods are a candidate for quantum speed-ups in supervised machine learning. The number of quantum measurements $N$ required for a reasonable kernel estimate is a critical resource, both from complexity considerations and because of the constraints of near-term quantum hardware. We emphasize that for classification tasks, the aim is accurate classification and not accurate kernel evaluation, and demonstrate that the former is more resource efficient. In general, the uncertainty in the quantum kernel, arising from finite sampling, leads to misclassifications over some kernel instantiations. We introduce a suitable performance metric that characterizes the robustness or reliability of classification over a dataset, and obtain a bound for $N$ which ensures, with high probability, that classification errors over a dataset are bounded by the margin errors of an idealized quantum kernel classifier. Using techniques of robust optimization, we then show that the number of quantum measurements can be significantly reduced by a robust formulation of the original support vector machine. We consider the SWAP test and the GATES test quantum circuits for kernel evaluations, and show that the SWAP test is always less reliable than the GATES test for any $N$. Our strategy is applicable to uncertainty in quantum kernels arising from {\em any} source of noise, although we only consider the statistical sampling noise in our analysis.