Abdourrahmane Mahamane Atto
LISTIC
Softlog-Softmax Layers and Divergences Contribute to a Computationally Dependable Ensemble Learning
Jun 04, 2025Abstract:The paper proposes a 4-step process for highlighting that softlog-softmax cascades can improve both consistency and dependability of the next generation ensemble learning systems. The first process is anatomical in nature: the target ensemble model under consideration is composed by canonical elements relating to the definition of a convolutional frustum. No a priori is considered in the choice of canonical forms. Diversity is the main criterion for selecting these forms. It is shown that the more complex the problem, the more useful this ensemble diversity is. The second process is physiological and relates to neural engineering: a softlog is derived to both make weak logarithmic operations consistent and lead, through multiple softlog-softmax layers, to intermediate decisions in the sense of respecting the same class logic as that faced by the output layer. The third process concerns neural information theory: softlog-based entropy and divergence are proposed for the sake of constructing information measures yielding consistent values on closed intervals. These information measures are used to determine the relationships between individual and sub-community decisions in frustum diversitybased ensemble learning. The concluding process addresses the derivation of an informative performance tensor for the purpose of a reliable ensemble evaluation.
Parametric Rectified Power Sigmoid Units: Learning Nonlinear Neural Transfer Analytical Forms
Feb 05, 2021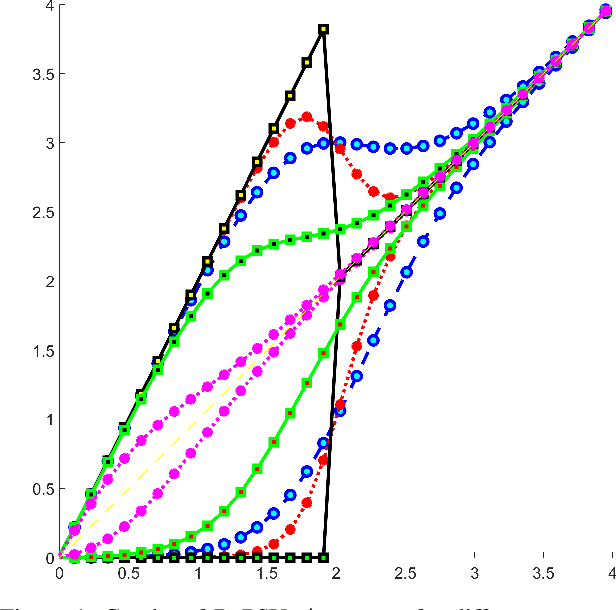
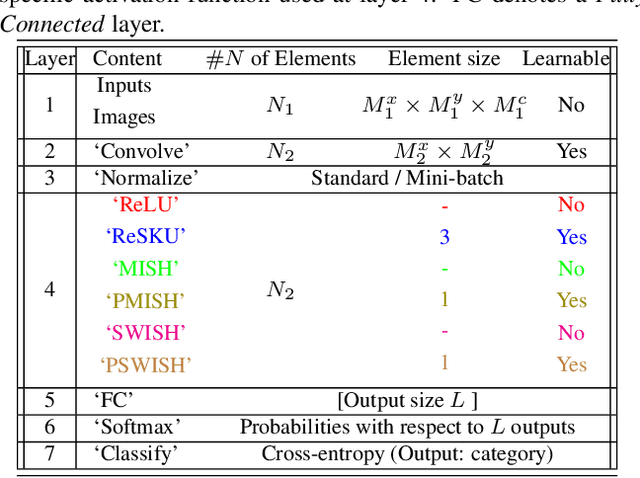
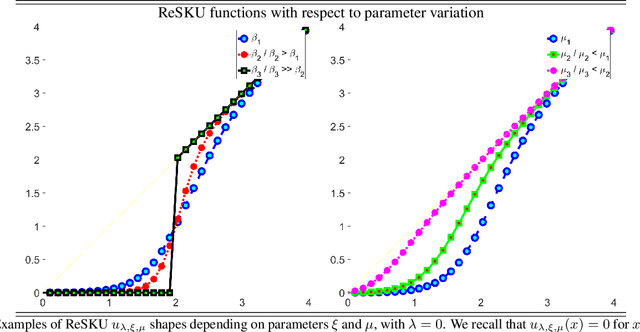
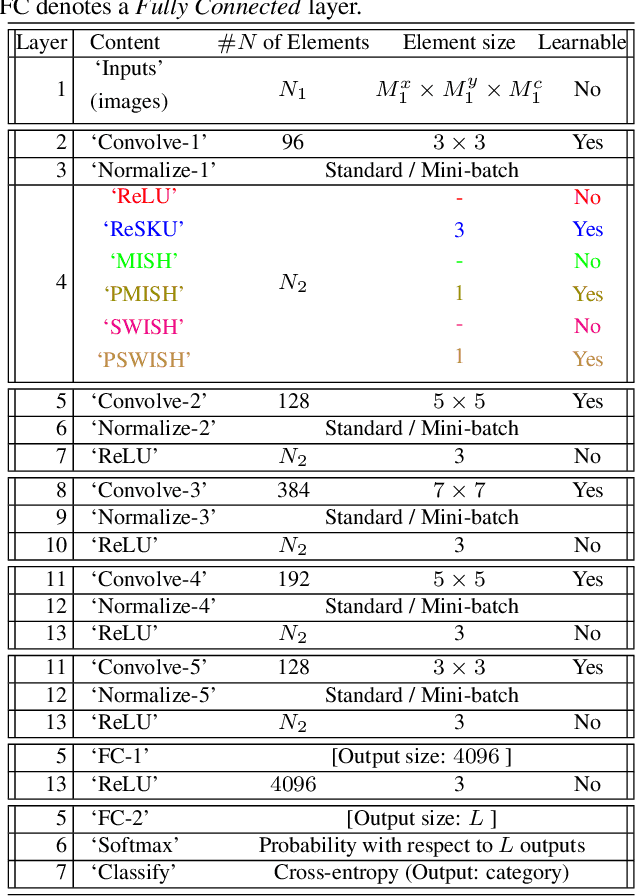
Abstract:The paper proposes representation functionals in a dual paradigm where learning jointly concerns both linear convolutional weights and parametric forms of nonlinear activation functions. The nonlinear forms proposed for performing the functional representation are associated with a new class of parametric neural transfer functions called rectified power sigmoid units. This class is constructed to integrate both advantages of sigmoid and rectified linear unit functions, in addition with rejecting the drawbacks of these functions. Moreover, the analytic form of this new neural class involves scale, shift and shape parameters so as to obtain a wide range of activation shapes, including the standard rectified linear unit as a limit case. Parameters of this neural transfer class are considered as learnable for the sake of discovering the complex shapes that can contribute in solving machine learning issues. Performance achieved by the joint learning of convolutional and rectified power sigmoid learnable parameters are shown outstanding in both shallow and deep learning frameworks. This class opens new prospects with respect to machine learning in the sense that learnable parameters are not only attached to linear transformations, but also to suitable nonlinear operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge