Federated Learning: From Theory to Practice

This book offers a hands-on introduction to building and understanding federated learning (FL) systems. FL enables multiple devices -- such as smartphones, sensors, or local computers -- to collaboratively train machine learning (ML) models, while keeping their data private and local. It is a powerful solution when data cannot or should not be centralized due to privacy, regulatory, or technical reasons. The book is designed for students, engineers, and researchers who want to learn how to design scalable, privacy preserving FL systems. Our main focus is on personalization: enabling each device to train its own model while still benefiting from collaboration with relevant devices. This is achieved by leveraging similarities between (the learning tasks associated with) devices that are encoded by the weighted edges (or links) of a federated learning network (FL network). The key idea is to represent real-world FL systems as networks of devices, where nodes correspond to device and edges represent communication links and data similarities between them. The training of personalized models for these devices can be naturally framed as a distributed optimization problem. This optimization problem is referred to as generalized total variation minimization (GTVMin) and ensures that devices with similar learning tasks learn similar model parameters. Our approach is both mathematically principled and practically motivated. While we introduce some advanced ideas from optimization theory and graph-based learning, we aim to keep the book accessible. Readers are guided through the core ideas step by step, with intuitive explanations.

Analysis of Total Variation Minimization for Clustered Federated Learning

A key challenge in federated learning applications is the statistical heterogeneity of local datasets. Clustered federated learning addresses this challenge by identifying clusters of local datasets that are approximately homogeneous. One recent approach to clustered federated learning is generalized total variation minimization (GTVMin). This approach requires a similarity graph which can be obtained by domain expertise or in a data-driven fashion via graph learning techniques. Under a widely applicable clustering assumption, we derive an upper bound the deviation between GTVMin solutions and their cluster-wise averages. This bound provides valuable insights into the effectiveness and robustness of GTVMin in addressing statistical heterogeneity within federated learning environments.

Towards Model-Agnostic Federated Learning over Networks

We present a model-agnostic federated learning method for decentralized data with an intrinsic network structure. The network structure reflects similarities between the (statistics of) local datasets and, in turn, their associated local models. Our method is an instance of empirical risk minimization, using a regularization term that is constructed from the network structure of data. In particular, we require well-connected local models, forming clusters, to yield similar predictions on a common test set. In principle our method can be applied to any collection of local models. The only restriction put on these local models is that they allow for efficient implementation of regularized empirical risk minimization (training). Such implementations might be available in the form of high-level programming frameworks such as \texttt{scikit-learn}, \texttt{Keras} or \texttt{PyTorch}.

flow-based clustering and spectral clustering: a comparison

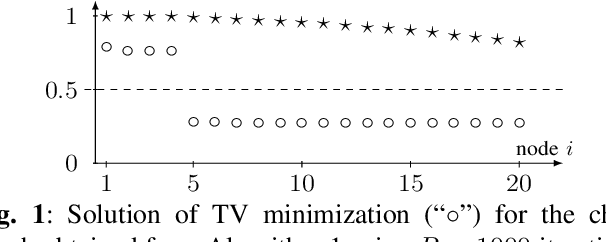
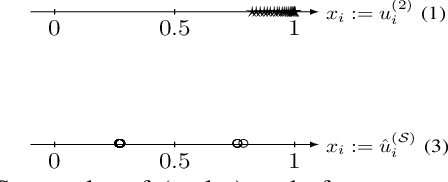
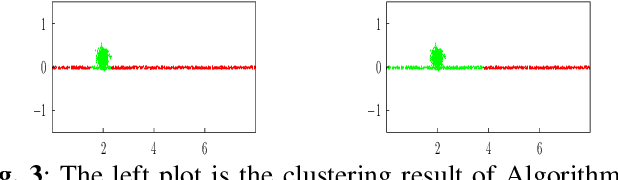
We propose and study a novel graph clustering method for data with an intrinsic network structure. Similar to spectral clustering, we exploit an intrinsic network structure of data to construct Euclidean feature vectors. These feature vectors can then be fed into basic clustering methods such as k-means or Gaussian mixture model (GMM) based soft clustering. What sets our approach apart from spectral clustering is that we do not use the eigenvectors of a graph Laplacian to construct the feature vectors. Instead, we use the solutions of total variation minimization problems to construct feature vectors that reflect connectivity between data points. Our motivation is that the solutions of total variation minimization are piece-wise constant around a given set of seed nodes. These seed nodes can be obtained from domain knowledge or by simple heuristics that are based on the network structure of data. Our results indicate that our clustering methods can cope with certain graph structures that are challenging for spectral clustering methods.

Federated Learning From Big Data Over Networks

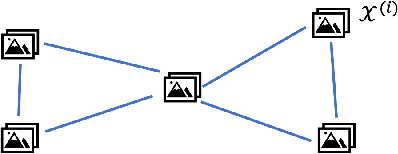
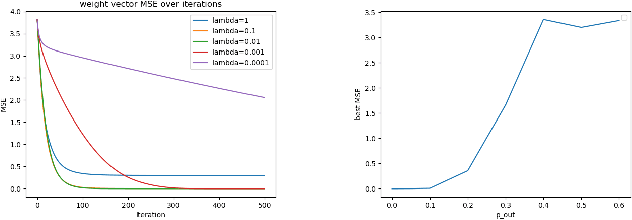
This paper formulates and studies a novel algorithm for federated learning from large collections of local datasets. This algorithm capitalizes on an intrinsic network structure that relates the local datasets via an undirected "empirical" graph. We model such big data over networks using a networked linear regression model. Each local dataset has individual regression weights. The weights of close-knit sub-collections of local datasets are enforced to deviate only little. This lends naturally to a network Lasso problem which we solve using a primal-dual method. We obtain a distributed federated learning algorithm via a message passing implementation of this primal-dual method. We provide a detailed analysis of the statistical and computational properties of the resulting federated learning algorithm.

Explainable Empirical Risk Minimization

The widespread use of modern machine learning methods in decision making crucially depends on their interpretability or explainability. The human users (decision makers) of machine learning methods are often not only interested in getting accurate predictions or projections. Rather, as a decision-maker, the user also needs a convincing answer (or explanation) to the question of why a particular prediction was delivered. Explainable machine learning might be a legal requirement when used for decision making with an immediate effect on the health of human beings. As an example consider the computer vision of a self-driving car whose predictions are used to decide if to stop the car. We have recently proposed an information-theoretic approach to construct personalized explanations for predictions obtained from ML. This method was model-agnostic and only required some training samples of the model to be explained along with a user feedback signal. This paper uses an information-theoretic measure for the quality of an explanation to learn predictors that are intrinsically explainable to a specific user. Our approach is not restricted to a particular hypothesis space, such as linear maps or shallow decision trees, whose predictor maps are considered as explainable by definition. Rather, we regularize an arbitrary hypothesis space using a personalized measure for the explainability of a particular predictor.