Deep learning for time series classification

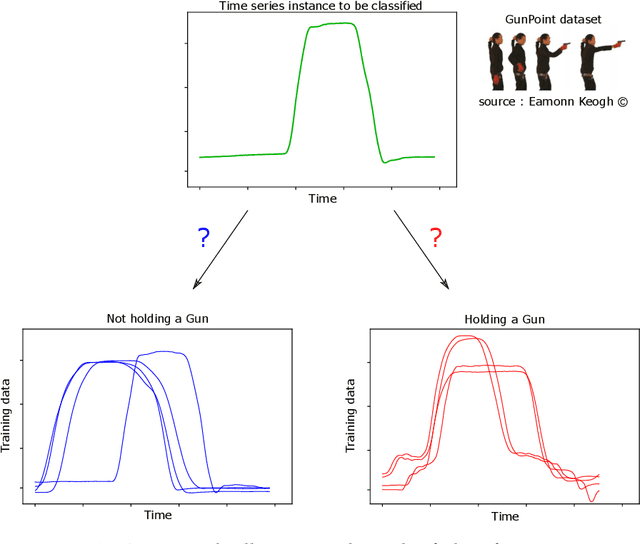
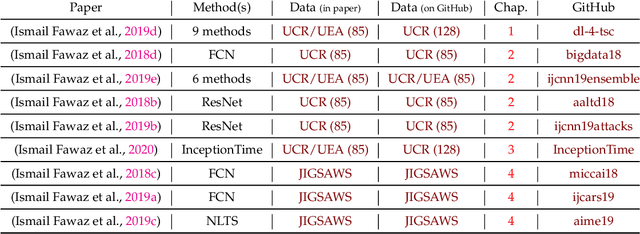
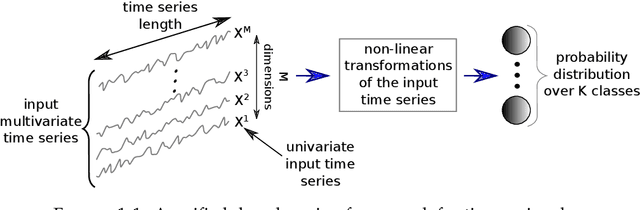
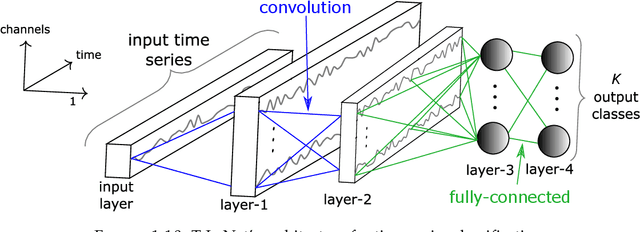
Time series analysis is a field of data science which is interested in analyzing sequences of numerical values ordered in time. Time series are particularly interesting because they allow us to visualize and understand the evolution of a process over time. Their analysis can reveal trends, relationships and similarities across the data. There exists numerous fields containing data in the form of time series: health care (electrocardiogram, blood sugar, etc.), activity recognition, remote sensing, finance (stock market price), industry (sensors), etc. Time series classification consists of constructing algorithms dedicated to automatically label time series data. The sequential aspect of time series data requires the development of algorithms that are able to harness this temporal property, thus making the existing off-the-shelf machine learning models for traditional tabular data suboptimal for solving the underlying task. In this context, deep learning has emerged in recent years as one of the most effective methods for tackling the supervised classification task, particularly in the field of computer vision. The main objective of this thesis was to study and develop deep neural networks specifically constructed for the classification of time series data. We thus carried out the first large scale experimental study allowing us to compare the existing deep methods and to position them compared other non-deep learning based state-of-the-art methods. Subsequently, we made numerous contributions in this area, notably in the context of transfer learning, data augmentation, ensembling and adversarial attacks. Finally, we have also proposed a novel architecture, based on the famous Inception network (Google), which ranks among the most efficient to date.

A tale of two toolkits, report the first: benchmarking time series classification algorithms for correctness and efficiency

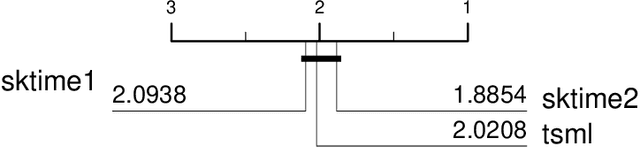
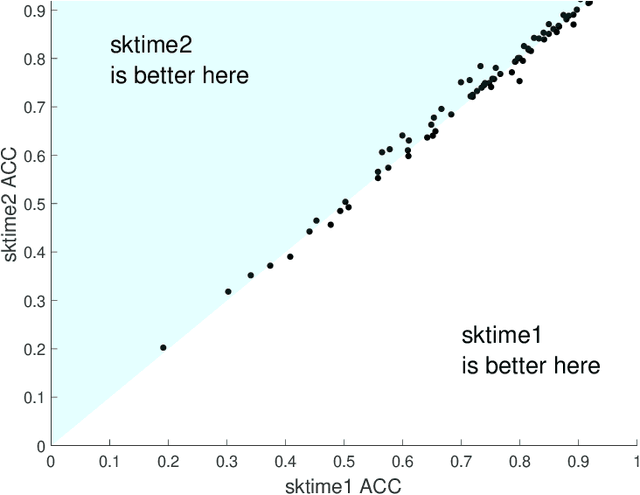
sktime is an open source, Python based, sklearn compatible toolkit for time series analysis developed by researchers at the University of East Anglia (UEA), University College London and the Alan Turing Institute. A key initial goal for sktime was to provide time series classification functionality equivalent to that available in a related java package, tsml, also developed at UEA. We describe the implementation of six such classifiers in sktime and compare them to their tsml equivalents. We demonstrate correctness through equivalence of accuracy on a range of standard test problems and compare the build time of the different implementations. We find that there is significant difference in accuracy on only one of the six algorithms we look at (Proximity Forest). This difference is causing us some pain in debugging. We found a much wider range of difference in efficiency. Again, this was not unexpected, but it does highlight ways both toolkits could be improved.

Online Debiasing for Adaptively Collected High-dimensional Data

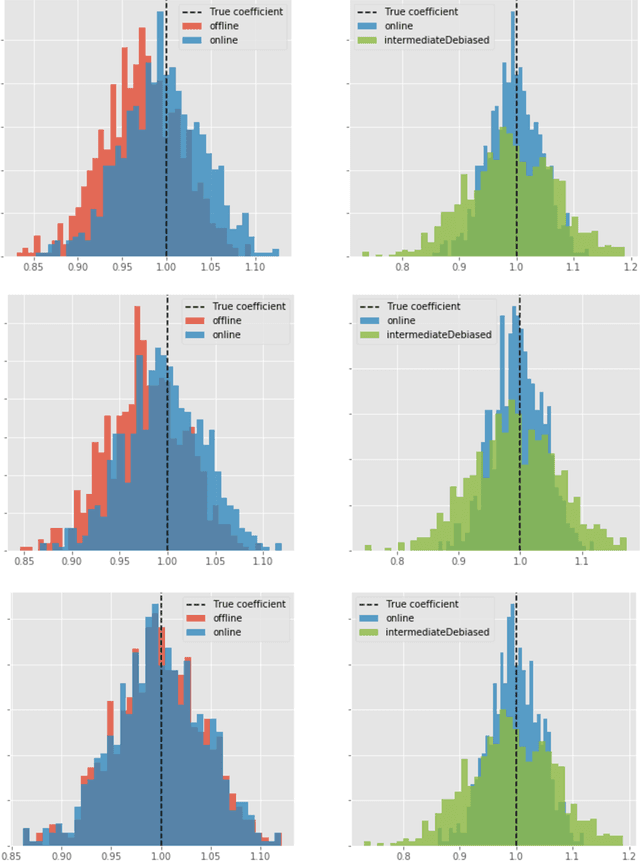
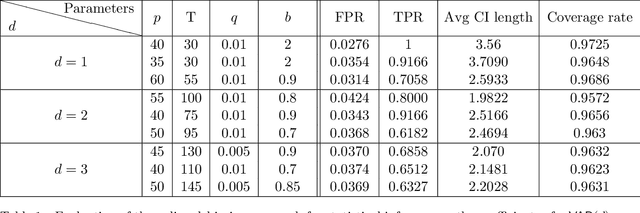
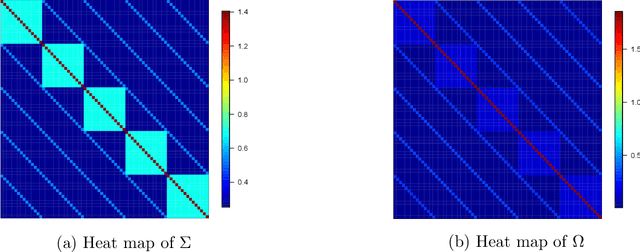
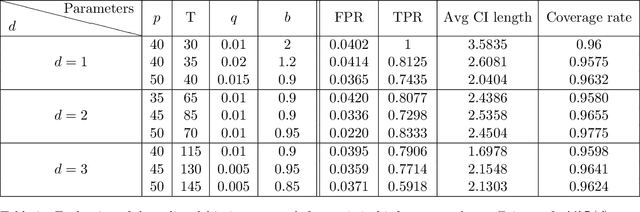
Adaptive collection of data is commonplace in applications throughout science and engineering. From the point of view of statistical inference however, adaptive data collection induces memory and correlation in the sample, and poses significant challenge. We consider the high-dimensional linear regression, where the sample is collected adaptively, and the sample size $n$ can be smaller than $p$, the number of covariates. In this setting, there are two distinct sources of bias: the first due to regularization imposed for consistent estimation, e.g. using the LASSO, and the second due to adaptivity in collecting the sample. We propose \emph{`online debiasing'}, a general procedure for estimators such as the LASSO, which addresses both sources of bias. In two concrete contexts $(i)$ batched data collection and $(ii)$ time series analysis, we demonstrate that online debiasing optimally debiases the LASSO estimate when the underlying parameter $\theta_0$ has sparsity of order $o(\sqrt{n}/\log p)$. In this regime, the debiased estimator can be used to compute $p$-values and confidence intervals of optimal size.

Nonparametric Extrema Analysis in Time Series for Envelope Extraction, Peak Detection and Clustering

In this paper, we propose a nonparametric approach that can be used in envelope extraction, peak-burst detection and clustering in time series. Our problem formalization results in a naturally defined splitting/forking of the time series. With a possibly hierarchical implementation, it can be used for various applications in machine learning, signal processing and mathematical finance. From an incoming input signal, our iterative procedure sequentially creates two signals (one upper bounding and one lower bounding signal) by minimizing the cumulative $L_1$ drift. We show that a solution can be efficiently calculated by use of a Viterbi-like path tracking algorithm together with an optimal elimination rule. We consider many interesting settings, where our algorithm has near-linear time complexities.

Deep Fusion of Lead-lag Graphs:Application to Cryptocurrencies

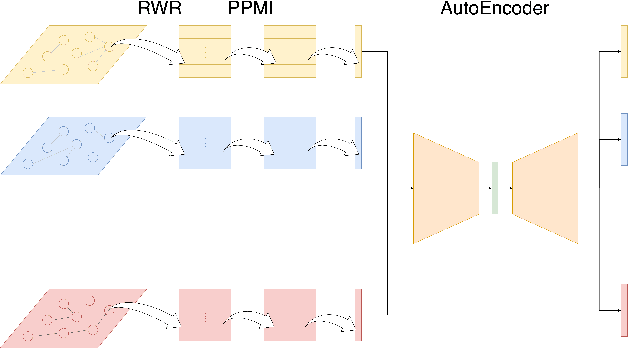
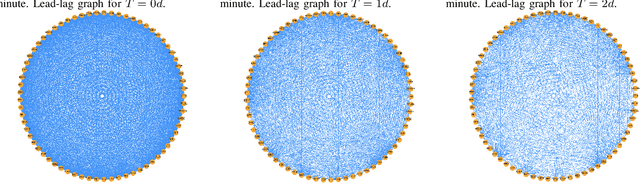
The study of time series has motivated many researchers, particularly on the area of multivariate-analysis. The study of co-movements and dependency between random variables leads us to develop metrics to describe existing connection between assets. The most commonly used are correlation and causality. Despite the growing literature, some connections remained still undetected. The objective of this paper is to propose a new representation learning algorithm capable to integrate synchronous and asynchronous relationships.

Predicting Student Performance in an Educational Game Using a Hidden Markov Model

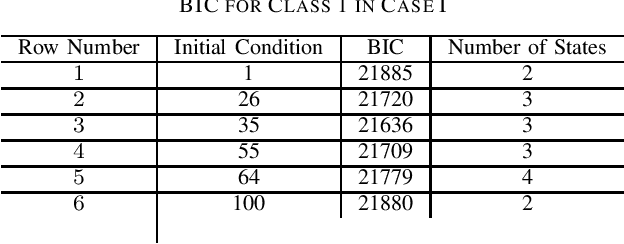
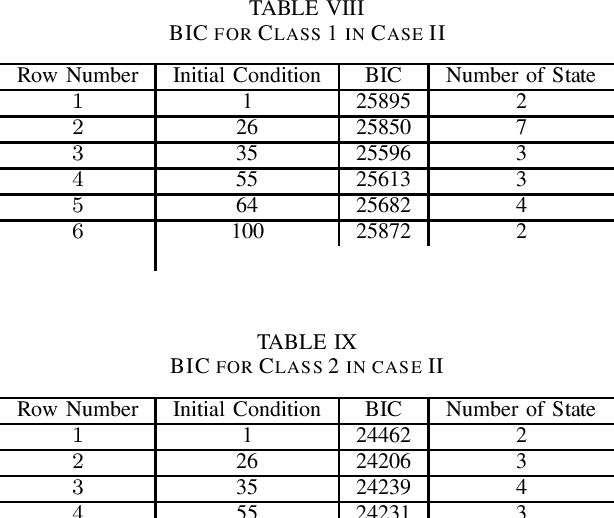
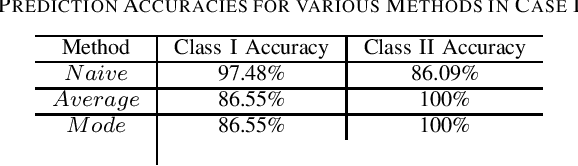
Contributions: Prior studies on education have mostly followed the model of the cross sectional study, namely, examining the pretest and the posttest scores. This paper shows that students' knowledge throughout the intervention can be estimated by time series analysis using a hidden Markov model. Background: Analyzing time series and the interaction between the students and the game data can result in valuable information that cannot be gained by only cross sectional studies of the exams. Research Questions: Can a hidden Markov model be used to analyze the educational games? Can a hidden Markov model be used to make a prediction of the students' performance? Methodology: The study was conducted on (N=854) students who played the Save Patch game. Students were divided into class 1 and class 2. Class 1 students are those who scored lower in the test than class 2 students. The analysis is done by choosing various features of the game as the observations. Findings: The state trajectories can predict the students' performance accurately for both class 1 and class 2.

RobustTrend: A Huber Loss with a Combined First and Second Order Difference Regularization for Time Series Trend Filtering

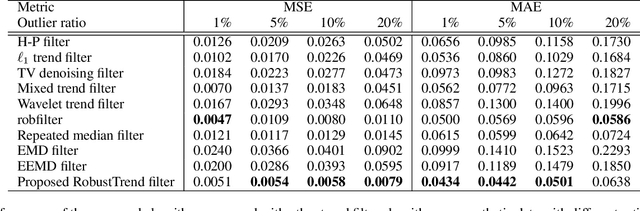
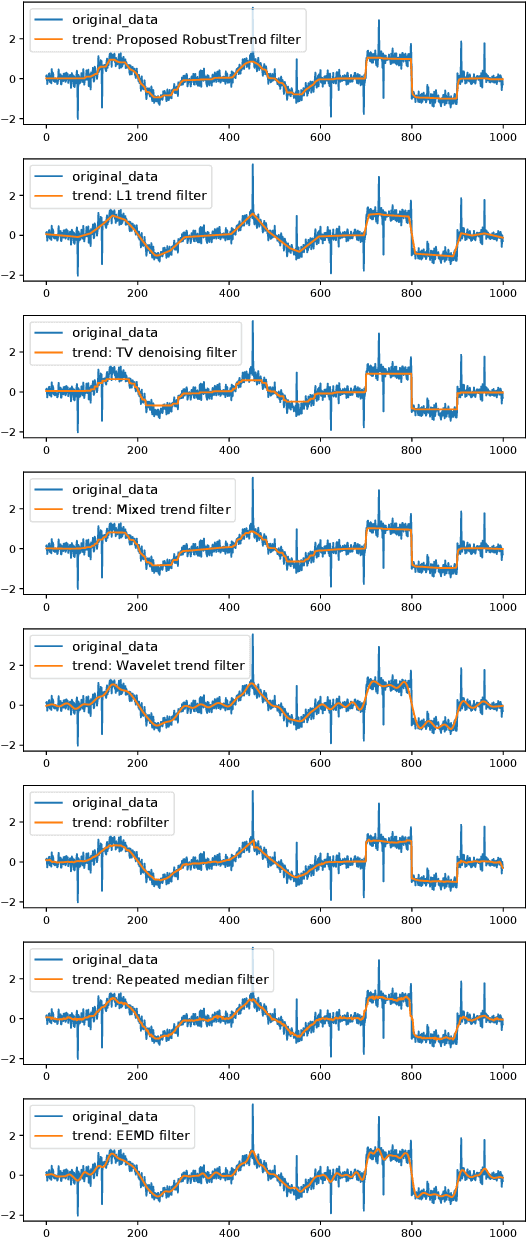
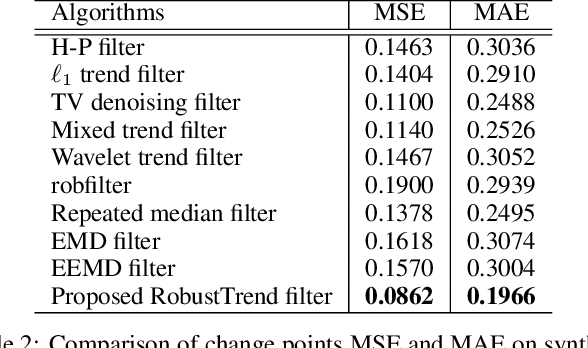
Extracting the underlying trend signal is a crucial step to facilitate time series analysis like forecasting and anomaly detection. Besides noise signal, time series can contain not only outliers but also abrupt trend changes in real-world scenarios. To deal with these challenges, we propose a robust trend filtering algorithm based on robust statistics and sparse learning. Specifically, we adopt the Huber loss to suppress outliers, and utilize a combination of the first order and second order difference on the trend component as regularization to capture both slow and abrupt trend changes. Furthermore, an efficient method is designed to solve the proposed robust trend filtering based on majorization minimization (MM) and alternative direction method of multipliers (ADMM). We compared our proposed robust trend filter with other nine state-of-the-art trend filtering algorithms on both synthetic and real-world datasets. The experiments demonstrate that our algorithm outperforms existing methods.

Transformers in Time Series: A Survey

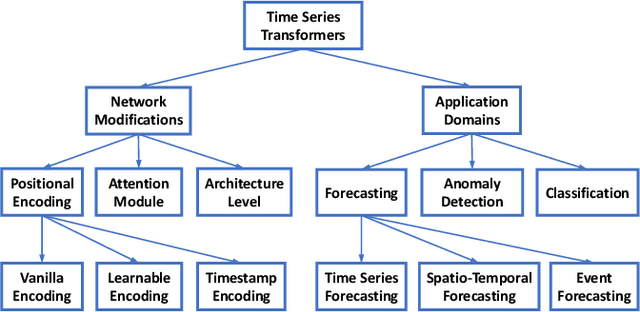
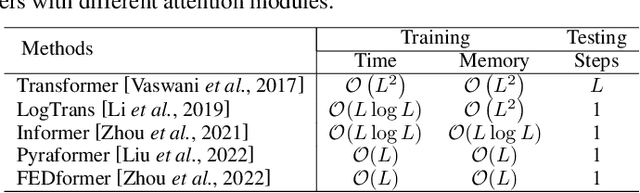
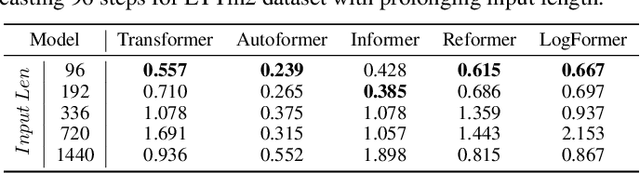
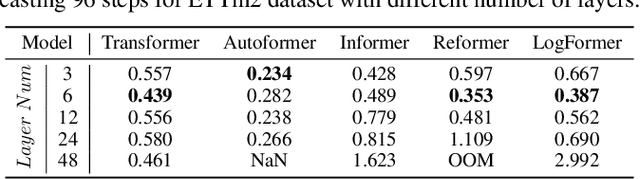
Transformers have achieved superior performances in many tasks in natural language processing and computer vision, which also intrigues great interests in the time series community. Among multiple advantages of transformers, the ability to capture long-range dependencies and interactions is especially attractive for time series modeling, leading to exciting progress in various time series applications. In this paper, we systematically review transformer schemes for time series modeling by highlighting their strengths as well as limitations through a new taxonomy to summarize existing time series transformers in two perspectives. From the perspective of network modifications, we summarize the adaptations of module level and architecture level of the time series transformers. From the perspective of applications, we categorize time series transformers based on common tasks including forecasting, anomaly detection, and classification. Empirically, we perform robust analysis, model size analysis, and seasonal-trend decomposition analysis to study how Transformers perform in time series. Finally, we discuss and suggest future directions to provide useful research guidance. A corresponding resource list that will be continuously updated can be found in the GitHub repository. To the best of our knowledge, this paper is the first work to comprehensively and systematically summarize the recent advances of Transformers for modeling time series data. We hope this survey will ignite further research interests in time series Transformers.

Identification of Abnormal States in Videos of Ants Undergoing Social Phase Change

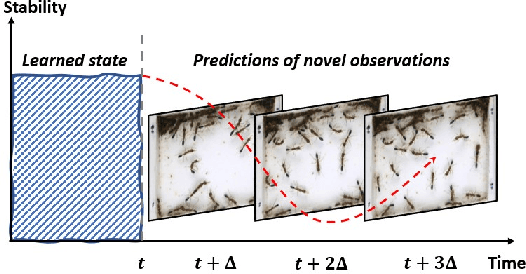
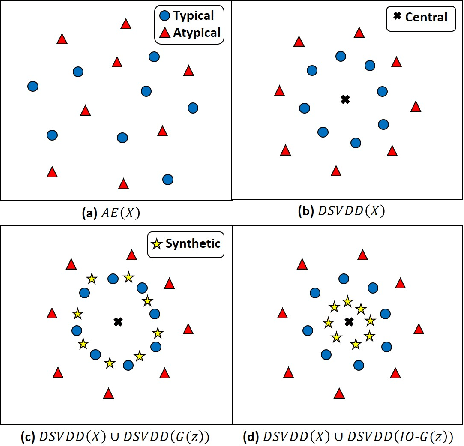
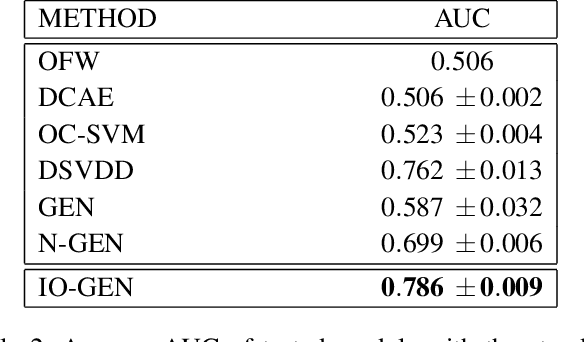
Biology is both an important application area and a source of motivation for development of advanced machine learning techniques. Although much attention has been paid to large and complex data sets resulting from high-throughput sequencing, advances in high-quality video recording technology have begun to generate similarly rich data sets requiring sophisticated techniques from both computer vision and time-series analysis. Moreover, just as studying gene expression patterns in one organism can reveal general principles that apply to other organisms, the study of complex social interactions in an experimentally tractable model system, such as a laboratory ant colony, can provide general principles about the dynamics many other social groups. Here, we focus on one such example from the study of reproductive regulation in small laboratory colonies of $\sim$50 Harpgenathos ants. These ants can be artificially induced to begin a $\sim$20 day process of hierarchy reformation. Although the conclusion of this process is conspicuous to a human observer, it is still unclear which behaviors during the transients are contributing to the process. To address this issue, we explore the potential application of One-class Classification (OC) to the detection of abnormal states in ant colonies for which behavioral data is only available for the normal societal conditions during training. Specifically, we build upon the Deep Support Vector Data Description (DSVDD) and introduce the Inner-Outlier Generator (IO-GEN) that synthesizes fake "inner outlier" observations during training that are near the center of the DSVDD data description. We show that IO-GEN increases the reliability of the final OC classifier relative to other DSVDD baselines. This method can be used to screen video frames for which additional human observation is needed.