Markov Chain Monte Carlo for Continuous-Time Switching Dynamical Systems

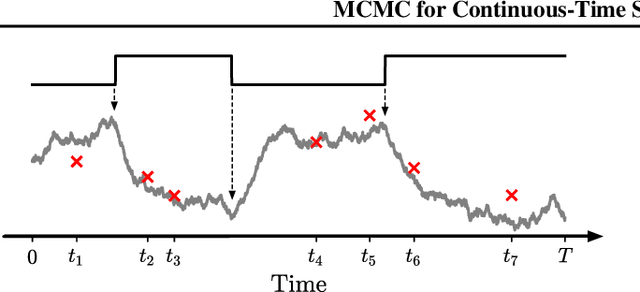
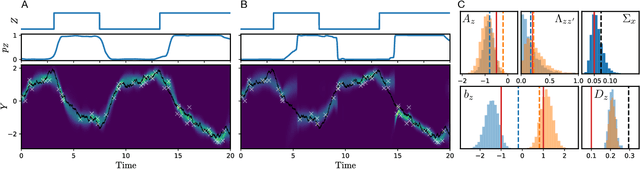
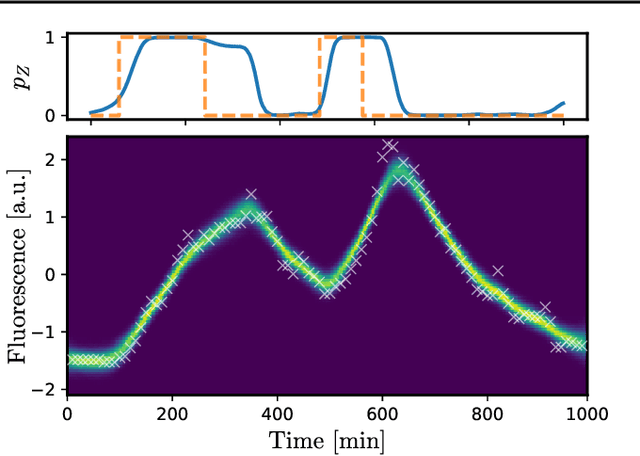
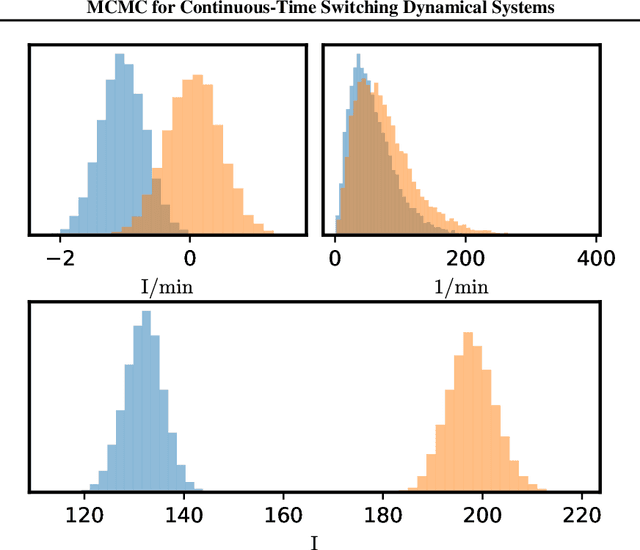
Switching dynamical systems are an expressive model class for the analysis of time-series data. As in many fields within the natural and engineering sciences, the systems under study typically evolve continuously in time, it is natural to consider continuous-time model formulations consisting of switching stochastic differential equations governed by an underlying Markov jump process. Inference in these types of models is however notoriously difficult, and tractable computational schemes are rare. In this work, we propose a novel inference algorithm utilizing a Markov Chain Monte Carlo approach. The presented Gibbs sampler allows to efficiently obtain samples from the exact continuous-time posterior processes. Our framework naturally enables Bayesian parameter estimation, and we also include an estimate for the diffusion covariance, which is oftentimes assumed fixed in stochastic differential equation models. We evaluate our framework under the modeling assumption and compare it against an existing variational inference approach.

Learning Disentangled Representations for Time Series

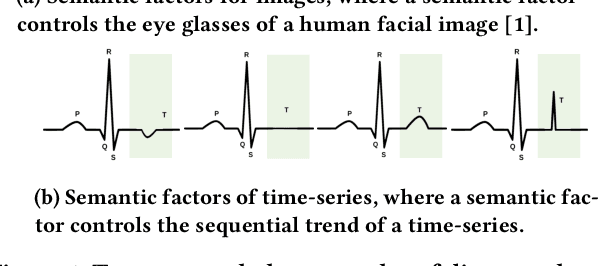
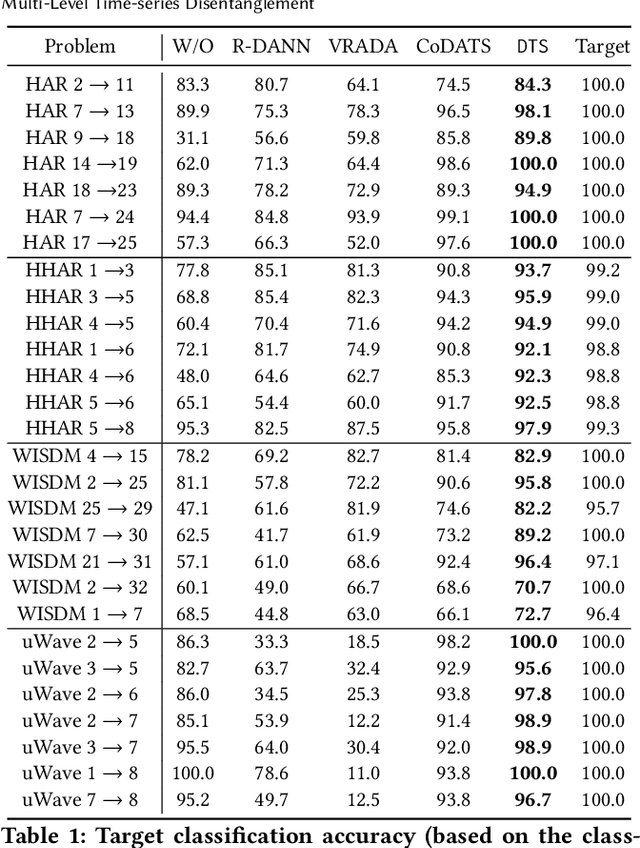
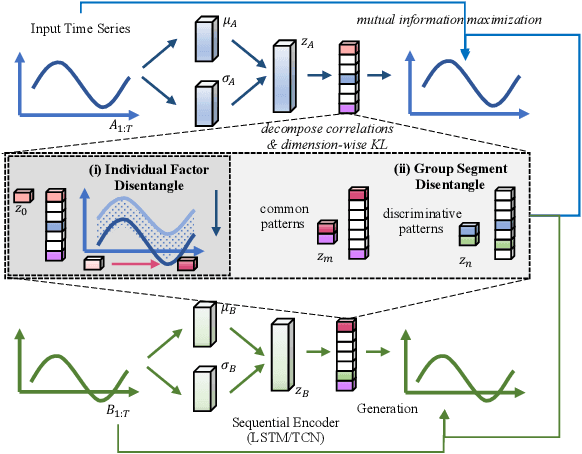
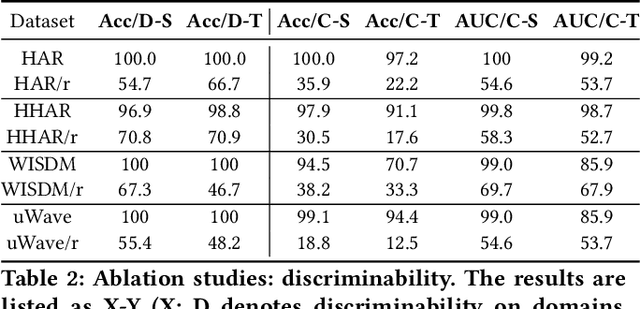
Time-series representation learning is a fundamental task for time-series analysis. While significant progress has been made to achieve accurate representations for downstream applications, the learned representations often lack interpretability and do not expose semantic meanings. Different from previous efforts on the entangled feature space, we aim to extract the semantic-rich temporal correlations in the latent interpretable factorized representation of the data. Motivated by the success of disentangled representation learning in computer vision, we study the possibility of learning semantic-rich time-series representations, which remains unexplored due to three main challenges: 1) sequential data structure introduces complex temporal correlations and makes the latent representations hard to interpret, 2) sequential models suffer from KL vanishing problem, and 3) interpretable semantic concepts for time-series often rely on multiple factors instead of individuals. To bridge the gap, we propose Disentangle Time Series (DTS), a novel disentanglement enhancement framework for sequential data. Specifically, to generate hierarchical semantic concepts as the interpretable and disentangled representation of time-series, DTS introduces multi-level disentanglement strategies by covering both individual latent factors and group semantic segments. We further theoretically show how to alleviate the KL vanishing problem: DTS introduces a mutual information maximization term, while preserving a heavier penalty on the total correlation and the dimension-wise KL to keep the disentanglement property. Experimental results on various real-world benchmark datasets demonstrate that the representations learned by DTS achieve superior performance in downstream applications, with high interpretability of semantic concepts.

On Merging Feature Engineering and Deep Learning for Diagnosis, Risk-Prediction and Age Estimation Based on the 12-Lead ECG

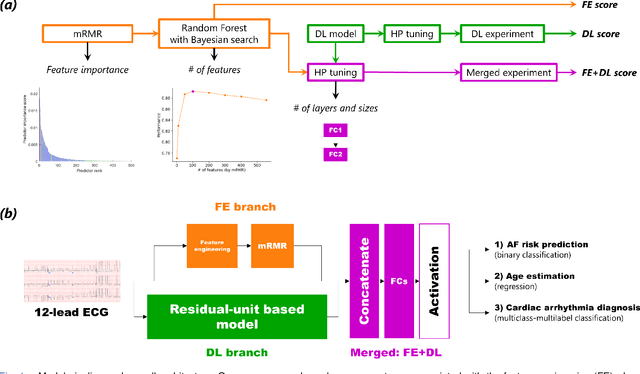
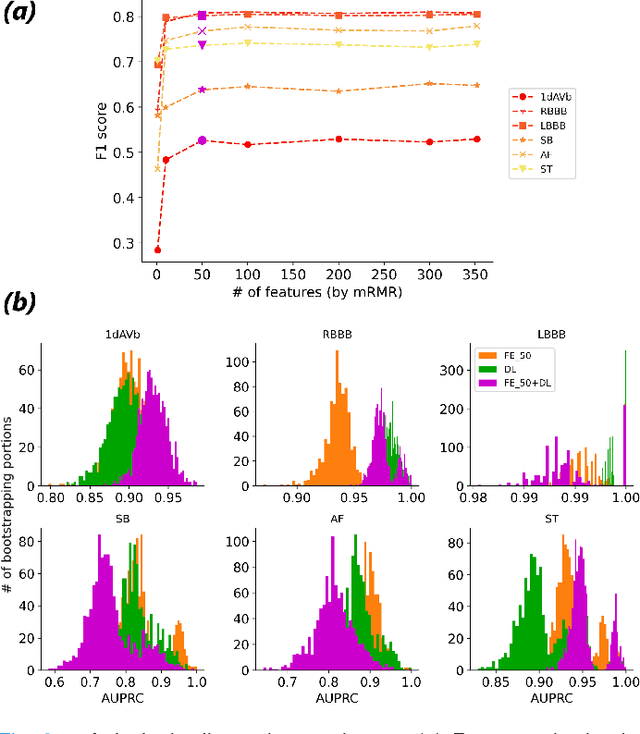
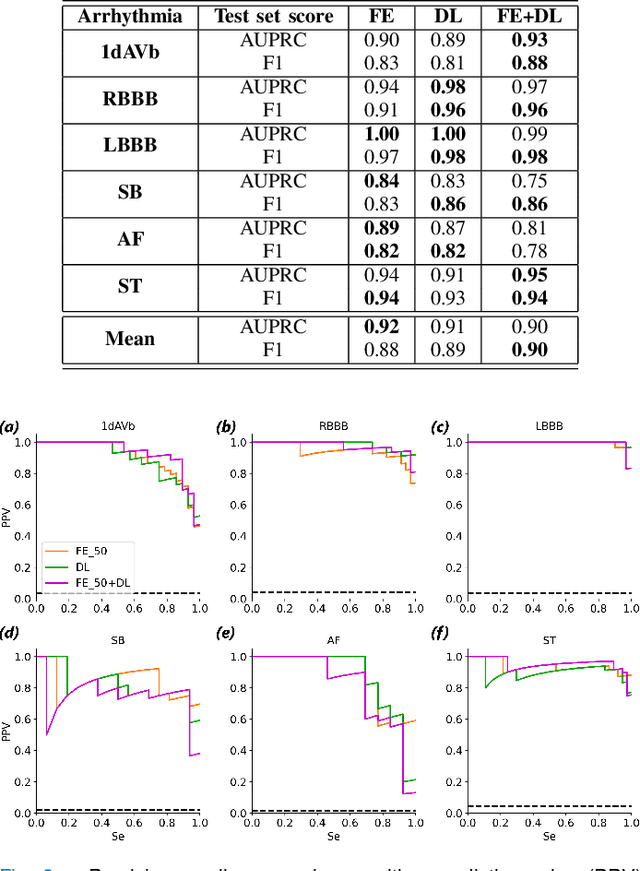
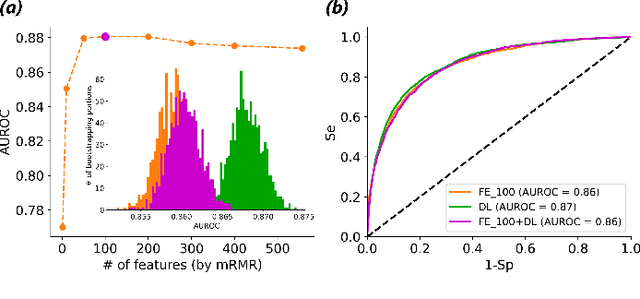
Objective: Machine learning techniques have been used extensively for 12-lead electrocardiogram (ECG) analysis. For physiological time series, deep learning (DL) superiority to feature engineering (FE) approaches based on domain knowledge is still an open question. Moreover, it remains unclear whether combining DL with FE may improve performance. Methods: We considered three tasks intending to address these research gaps: cardiac arrhythmia diagnosis (multiclass-multilabel classification), atrial fibrillation risk prediction (binary classification), and age estimation (regression). We used an overall dataset of 2.3M 12-lead ECG recordings to train the following models for each task: i) a random forest taking the FE as input was trained as a classical machine learning approach; ii) an end-to-end DL model; and iii) a merged model of FE+DL. Results: FE yielded comparable results to DL while necessitating significantly less data for the two classification tasks and it was outperformed by DL for the regression task. For all tasks, merging FE with DL did not improve performance over DL alone. Conclusion: We found that for traditional 12-lead ECG based diagnosis tasks DL did not yield a meaningful improvement over FE, while it improved significantly the nontraditional regression task. We also found that combining FE with DL did not improve over DL alone which suggests that the FE were redundant with the features learned by DL. Significance: Our findings provides important recommendations on what machine learning strategy and data regime to chose with respect to the task at hand for the development of new machine learning models based on the 12-lead ECG.

Interpretable Time-series Representation Learning With Multi-Level Disentanglement

Time-series representation learning is a fundamental task for time-series analysis. While significant progress has been made to achieve accurate representations for downstream applications, the learned representations often lack interpretability and do not expose semantic meanings. Different from previous efforts on the entangled feature space, we aim to extract the semantic-rich temporal correlations in the latent interpretable factorized representation of the data. Motivated by the success of disentangled representation learning in computer vision, we study the possibility of learning semantic-rich time-series representations, which remains unexplored due to three main challenges: 1) sequential data structure introduces complex temporal correlations and makes the latent representations hard to interpret, 2) sequential models suffer from KL vanishing problem, and 3) interpretable semantic concepts for time-series often rely on multiple factors instead of individuals. To bridge the gap, we propose Disentangle Time Series (DTS), a novel disentanglement enhancement framework for sequential data. Specifically, to generate hierarchical semantic concepts as the interpretable and disentangled representation of time-series, DTS introduces multi-level disentanglement strategies by covering both individual latent factors and group semantic segments. We further theoretically show how to alleviate the KL vanishing problem: DTS introduces a mutual information maximization term, while preserving a heavier penalty on the total correlation and the dimension-wise KL to keep the disentanglement property. Experimental results on various real-world benchmark datasets demonstrate that the representations learned by DTS achieve superior performance in downstream applications, with high interpretability of semantic concepts.

Wasserstein multivariate auto-regressive models for modeling distributional time series and its application in graph learning

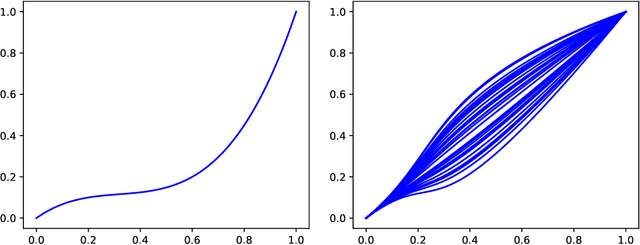
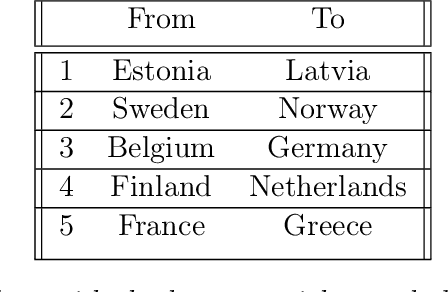
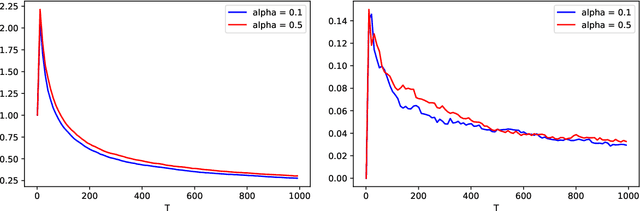
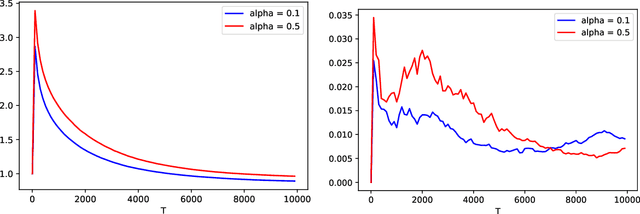
We propose a new auto-regressive model for the statistical analysis of multivariate distributional time series. The data of interest consist of a collection of multiple series of probability measures supported over a bounded interval of the real line, and that are indexed by distinct time instants. The probability measures are modelled as random objects in the Wasserstein space. We establish the auto-regressive model in the tangent space at the Lebesgue measure by first centering all the raw measures so that their Fr\'echet means turn to be the Lebesgue measure. Using the theory of iterated random function systems, results on the existence, uniqueness and stationarity of the solution of such a model are provided. We also propose a consistent estimator for the model coefficient. In addition to the analysis of simulated data, the proposed model is illustrated with two real data sets made of observations from age distribution in different countries and bike sharing network in Paris. Finally, due to the positive and boundedness constraints that we impose on the model coefficients, the proposed estimator that is learned under these constraints, naturally has a sparse structure. The sparsity allows furthermore the application of the proposed model in learning a graph of temporal dependency from the multivariate distributional time series.

Dynamics of information flow and engaging power of narratives in the polarised debate on vaccines

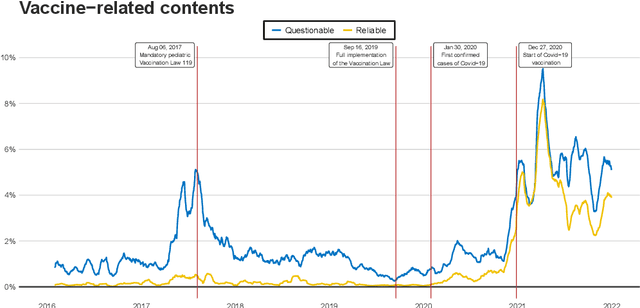
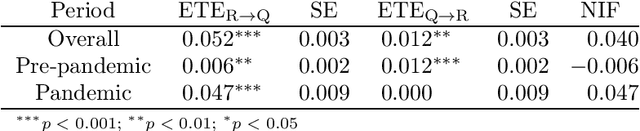
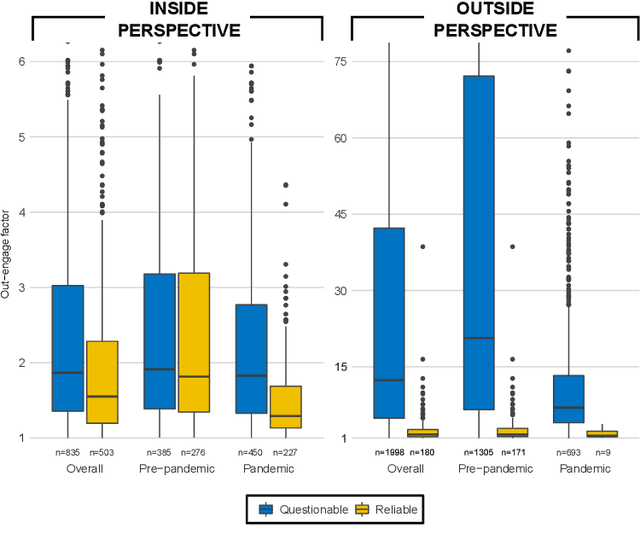
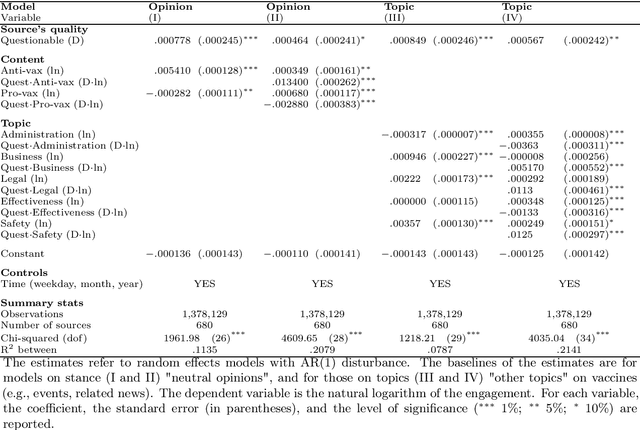
In this study we approach the complexity of the vaccine debate from a new and comprehensive perspective. Focusing on the Italian context, we examine almost all the online information produced in the 2016-2021 timeframe by both sources that have a reputation for misinformation and those that do not. Although reliable sources can rely on larger newsrooms and cover more news than misinformation ones, the transfer entropy analysis of the corresponding time series reveals that the former have not always informationally dominated the latter on the vaccine subject. Indeed, the pre-pandemic period sees misinformation establish itself as leader of the process, even in causal terms, and gain dramatically more user engagement than news from reliable sources. Despite this information gap was filled during the Covid-19 outbreak, the newfound leading role of reliable sources as drivers of the information ecosystem has only partially had a beneficial effect in reducing user engagement with misinformation on vaccines. Our results indeed show that, except for effectiveness of vaccination, reliable sources have never adequately countered the anti-vax narrative, specially in the pre-pandemic period, thus contributing to exacerbate science denial and belief in conspiracy theories. At the same time, however, they confirm the efficacy of assiduously proposing a convincing counter-narrative to misinformation spread. Indeed, effectiveness of vaccination turns out to be the least engaging topic discussed by misinformation during the pandemic period, when compared to other polarising arguments such as safety concerns, legal issues and vaccine business. By highlighting the strengths and weaknesses of institutional and mainstream communication, our findings can be a valuable asset for improving and better targeting campaigns against misinformation on vaccines.

Towards Safe Policy Improvement for Non-Stationary MDPs

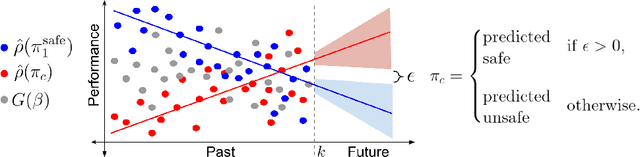
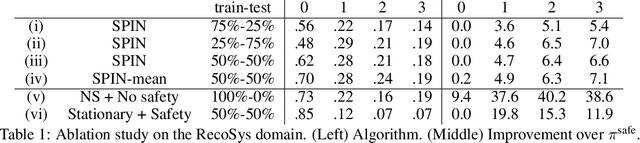
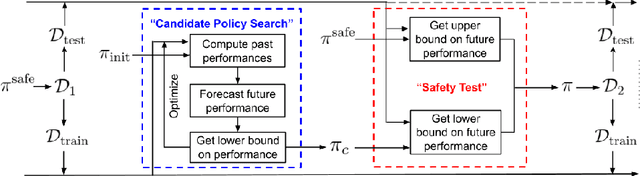
Many real-world sequential decision-making problems involve critical systems with financial risks and human-life risks. While several works in the past have proposed methods that are safe for deployment, they assume that the underlying problem is stationary. However, many real-world problems of interest exhibit non-stationarity, and when stakes are high, the cost associated with a false stationarity assumption may be unacceptable. We take the first steps towards ensuring safety, with high confidence, for smoothly-varying non-stationary decision problems. Our proposed method extends a type of safe algorithm, called a Seldonian algorithm, through a synthesis of model-free reinforcement learning with time-series analysis. Safety is ensured using sequential hypothesis testing of a policy's forecasted performance, and confidence intervals are obtained using wild bootstrap.

Nonstationary Temporal Matrix Factorization for Multivariate Time Series Forecasting

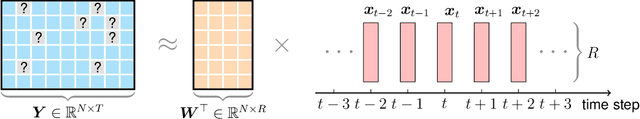
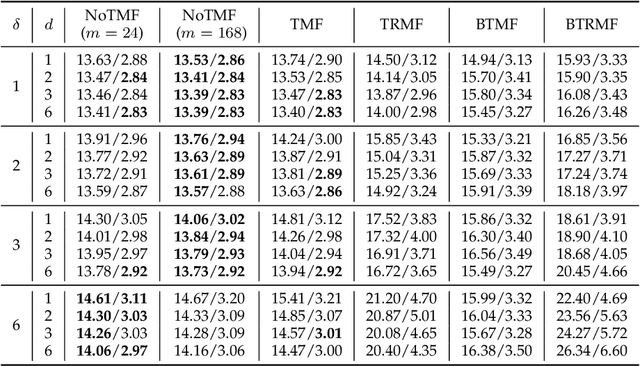
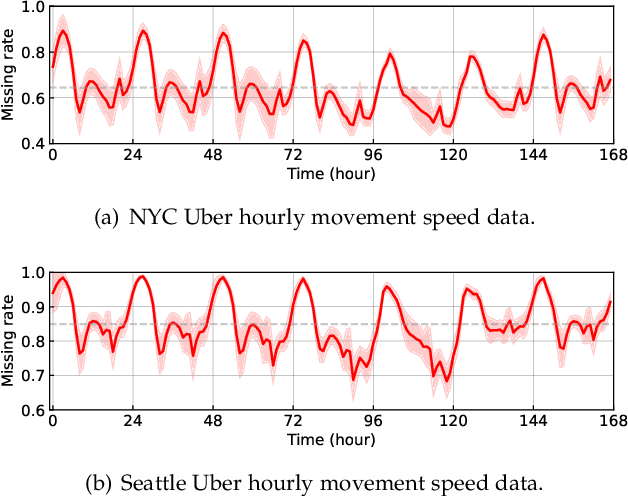
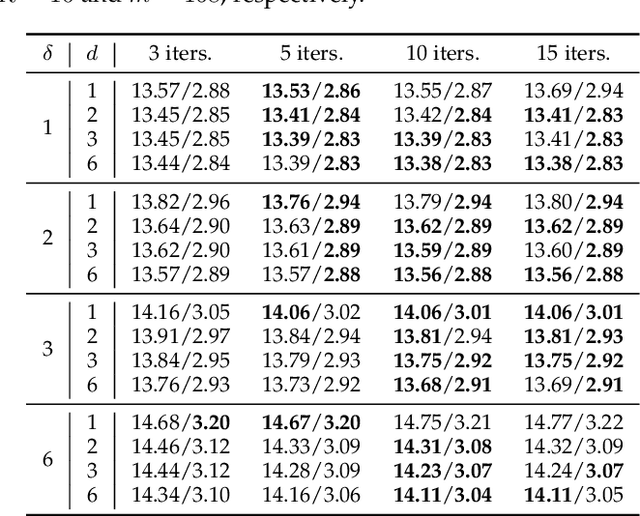
Modern time series datasets are often high-dimensional, incomplete/sparse, and nonstationary. These properties hinder the development of scalable and efficient solutions for time series forecasting and analysis. To address these challenges, we propose a Nonstationary Temporal Matrix Factorization (NoTMF) model, in which matrix factorization is used to reconstruct the whole time series matrix and vector autoregressive (VAR) process is imposed on a properly differenced copy of the temporal factor matrix. This approach not only preserves the low-rank property of the data but also offers consistent temporal dynamics. The learning process of NoTMF involves the optimization of two factor matrices and a collection of VAR coefficient matrices. To efficiently solve the optimization problem, we derive an alternating minimization framework, in which subproblems are solved using conjugate gradient and least squares methods. In particular, the use of conjugate gradient method offers an efficient routine and allows us to apply NoTMF on large-scale problems. Through extensive experiments on Uber movement speed dataset, we demonstrate the superior accuracy and effectiveness of NoTMF over other baseline models. Our results also confirm the importance of addressing the nonstationarity of real-world time series data such as spatiotemporal traffic flow/speed.

Regularized Bilinear Discriminant Analysis for Multivariate Time Series Data

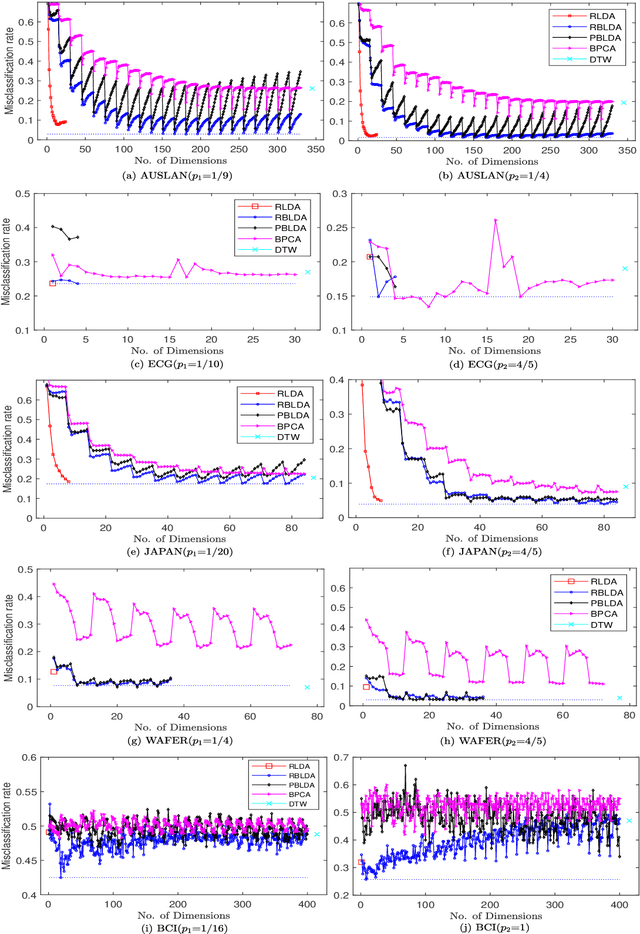
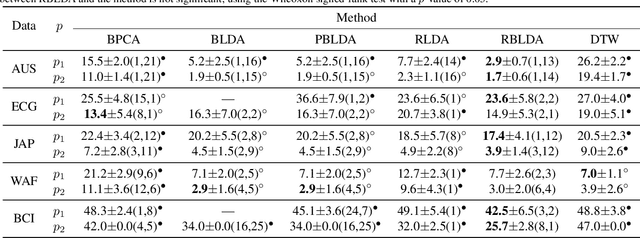
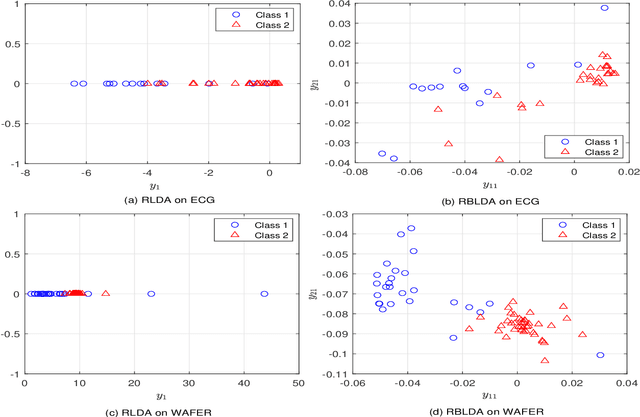
In recent years, the methods on matrix-based or bilinear discriminant analysis (BLDA) have received much attention. Despite their advantages, it has been reported that the traditional vector-based regularized LDA (RLDA) is still quite competitive and could outperform BLDA on some benchmark datasets. Nevertheless, it is also noted that this finding is mainly limited to image data. In this paper, we propose regularized BLDA (RBLDA) and further explore the comparison between RLDA and RBLDA on another type of matrix data, namely multivariate time series (MTS). Unlike image data, MTS typically consists of multiple variables measured at different time points. Although many methods for MTS data classification exist within the literature, there is relatively little work in exploring the matrix data structure of MTS data. Moreover, the existing BLDA can not be performed when one of its within-class matrices is singular. To address the two problems, we propose RBLDA for MTS data classification, where each of the two within-class matrices is regularized via one parameter. We develop an efficient implementation of RBLDA and an efficient model selection algorithm with which the cross validation procedure for RBLDA can be performed efficiently. Experiments on a number of real MTS data sets are conducted to evaluate the proposed algorithm and compare RBLDA with several closely related methods, including RLDA and BLDA. The results reveal that RBLDA achieves the best overall recognition performance and the proposed model selection algorithm is efficient; Moreover, RBLDA can produce better visualization of MTS data than RLDA.

Early Abandoning PrunedDTW and its application to similarity search

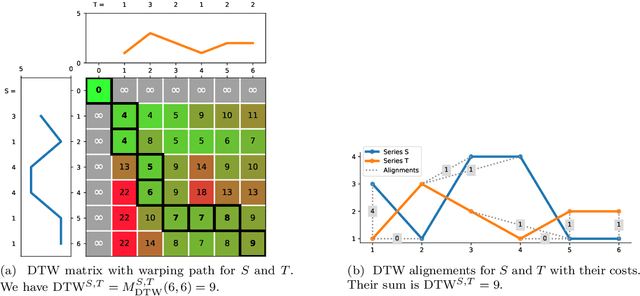
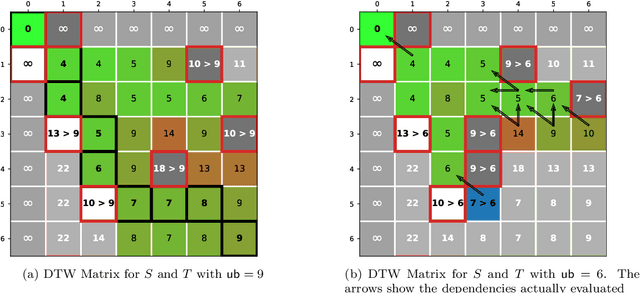
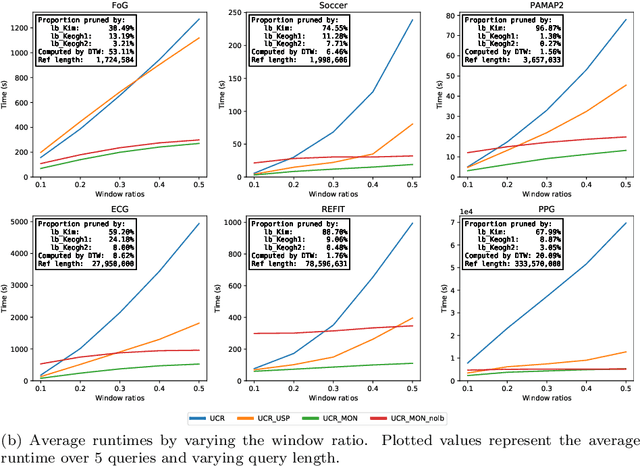
The Dynamic Time Warping ("DTW") distance is widely used in time series analysis, be it for classification, clustering or similarity search. However, its quadratic time complexity prevents it from scaling. Strategies, based on early abandoning DTW or skipping its computation altogether thanks to lower bounds, have been developed for certain use cases such as nearest neighbour search. But vectorization and approximation aside, no advance was made on DTW itself until recently with the introduction of PrunedDTW. This algorithm, able to prune unpromising alignments, was later fitted with early abandoning. We present a new version of PrunedDTW, "EAPrunedDTW", designed with early abandon in mind from the start, and able to early abandon faster than before. We show that EAPrunedDTW significantly improves the computation time of similarity search in the UCR Suite, and renders lower bounds dispensable.