"Time Series Analysis": models, code, and papers
Time Series Analysis via Matrix Estimation
Aug 24, 2018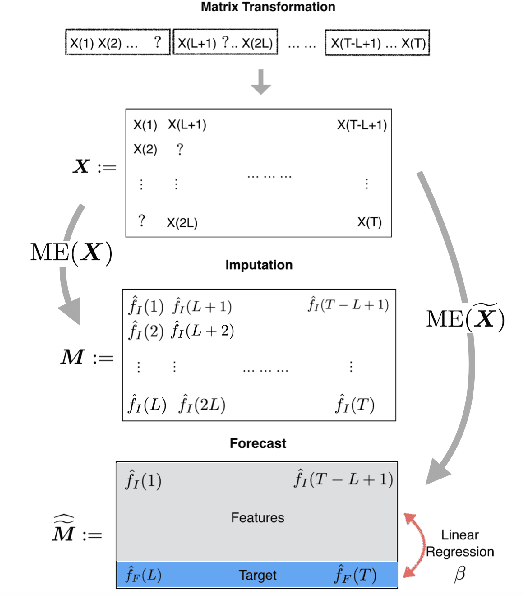
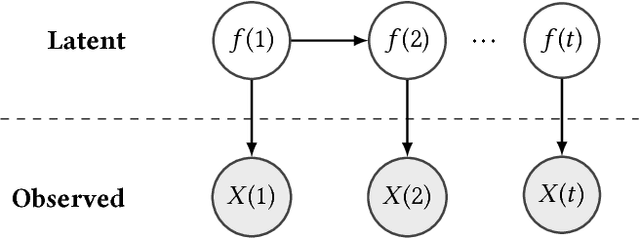
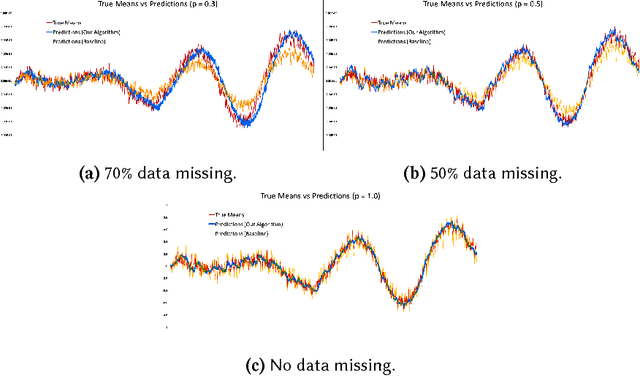
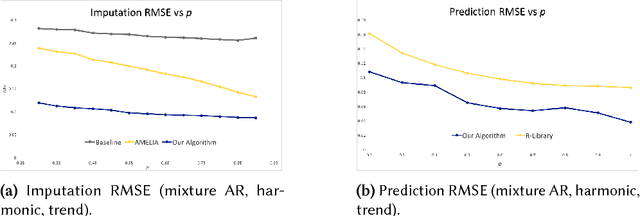
We propose an algorithm to impute and forecast a time series by transforming the observed time series into a matrix, utilizing matrix estimation to recover missing values and de-noise observed entries, and performing linear regression to make predictions. At the core of our analysis is a representation result, which states that for a large model class, the transformed matrix obtained from the time series via our algorithm is (approximately) low-rank. This, in effect, generalizes the widely used Singular Spectrum Analysis (SSA) in literature, and allows us to establish a rigorous link between time series analysis and matrix estimation. The key is to construct a matrix with non-overlapping entries rather than with the Hankel matrix as done in the literature, including in SSA. We provide finite sample analysis for imputation and prediction leading to the asymptotic consistency of our method. A salient feature of our algorithm is that it is model agnostic both with respect to the underlying time dynamics as well as the noise model in the observations. Being noise agnostic makes our algorithm applicable to the setting where the state is hidden and we only have access to its noisy observations a la a Hidden Markov Model, e.g., observing a Poisson process with a time-varying parameter without knowing that the process is Poisson, but still recovering the time-varying parameter accurately. As part of the forecasting algorithm, an important task is to perform regression with noisy observations of the features a la an error- in-variable regression. In essence, our approach suggests a matrix estimation based method for such a setting, which could be of interest in its own right. Through synthetic and real-world datasets, we demonstrate that our algorithm outperforms standard software packages (including R libraries) in the presence of missing data as well as high levels of noise.
Efficient and Consistent Robust Time Series Analysis
Jul 01, 2016
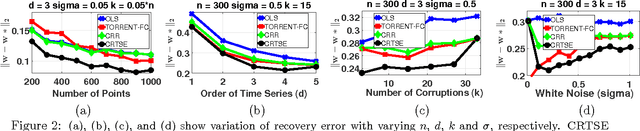
We study the problem of robust time series analysis under the standard auto-regressive (AR) time series model in the presence of arbitrary outliers. We devise an efficient hard thresholding based algorithm which can obtain a consistent estimate of the optimal AR model despite a large fraction of the time series points being corrupted. Our algorithm alternately estimates the corrupted set of points and the model parameters, and is inspired by recent advances in robust regression and hard-thresholding methods. However, a direct application of existing techniques is hindered by a critical difference in the time-series domain: each point is correlated with all previous points rendering existing tools inapplicable directly. We show how to overcome this hurdle using novel proof techniques. Using our techniques, we are also able to provide the first efficient and provably consistent estimator for the robust regression problem where a standard linear observation model with white additive noise is corrupted arbitrarily. We illustrate our methods on synthetic datasets and show that our methods indeed are able to consistently recover the optimal parameters despite a large fraction of points being corrupted.
Variable-lag Granger Causality and Transfer Entropy for Time Series Analysis
Mar 08, 2020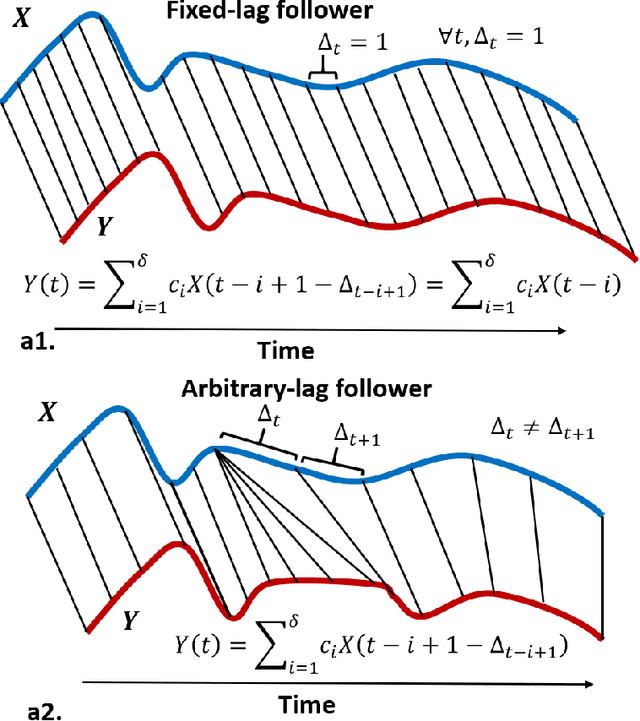
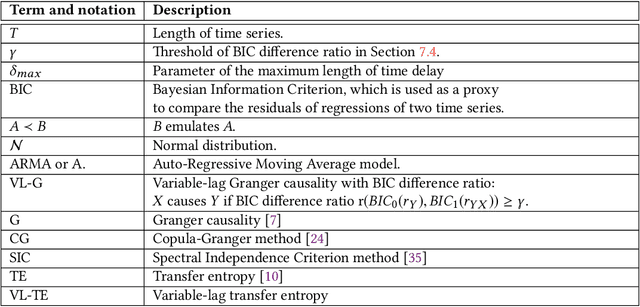
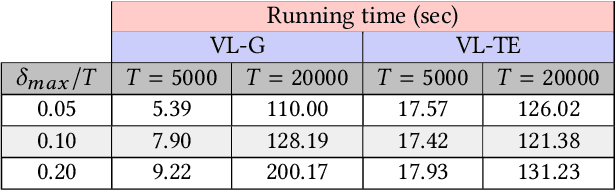
Granger causality is a fundamental technique for causal inference in time series data, commonly used in the social and biological sciences. Typical operationalizations of Granger causality make a strong assumption that every time point of the effect time series is influenced by a combination of other time series with a fixed time delay. The assumption of fixed time delay also exists in Transfer Entropy, which is considered to be a non-linear version of Granger causality. However, the assumption of the fixed time delay does not hold in many applications, such as collective behavior, financial markets, and many natural phenomena. To address this issue, we develop Variable-lag Granger causality and Variable-lag Transfer Entropy, generalizations of both Granger causality and Transfer Entropy that relax the assumption of the fixed time delay and allow causes to influence effects with arbitrary time delays. In addition, we propose a method for inferring both variable-lag Granger causality and Transfer Entropy relations. We demonstrate our approaches on an application for studying coordinated collective behavior and other real-world casual-inference datasets and show that our proposed approaches perform better than several existing methods in both simulated and real-world datasets. Our approaches can be applied in any domain of time series analysis. The software of this work is available in the R-CRAN package: VLTimeCausality.
Structured low-rank matrix completion for forecasting in time series analysis
Feb 22, 2018
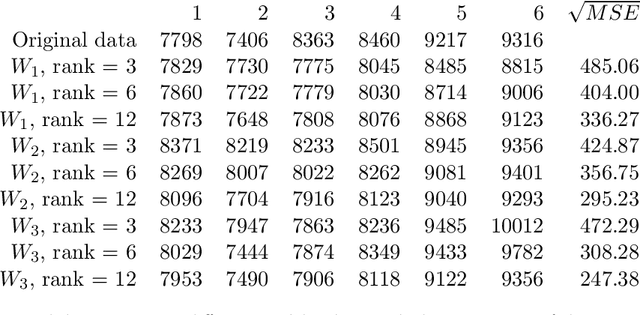
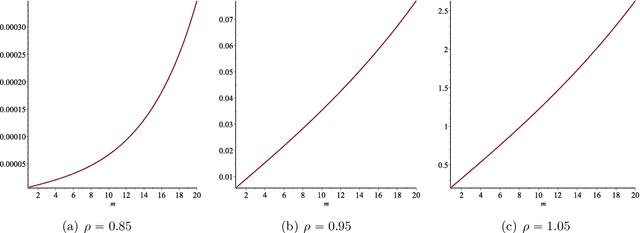
In this paper we consider the low-rank matrix completion problem with specific application to forecasting in time series analysis. Briefly, the low-rank matrix completion problem is the problem of imputing missing values of a matrix under a rank constraint. We consider a matrix completion problem for Hankel matrices and a convex relaxation based on the nuclear norm. Based on new theoretical results and a number of numerical and real examples, we investigate the cases when the proposed approach can work. Our results highlight the importance of choosing a proper weighting scheme for the known observations.
Time Series Analysis of Blockchain-Based Cryptocurrency Price Changes
Feb 19, 2022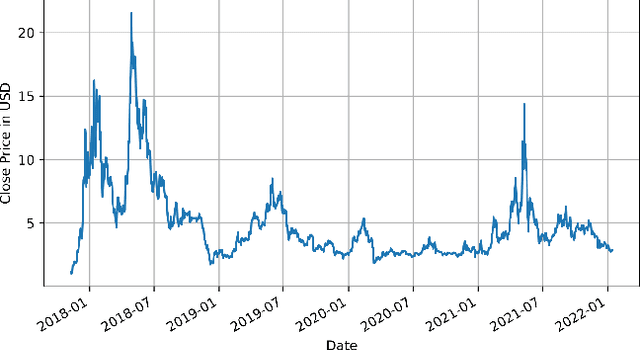
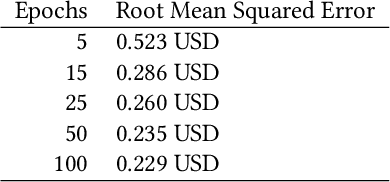
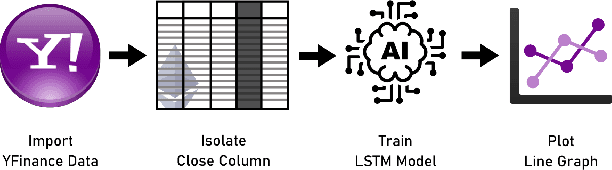

In this paper we apply neural networks and Artificial Intelligence (AI) to historical records of high-risk cryptocurrency coins to train a prediction model that guesses their price. This paper's code contains Jupyter notebooks, one of which outputs a timeseries graph of any cryptocurrency price once a CSV file of the historical data is inputted into the program. Another Jupyter notebook trains an LSTM, or a long short-term memory model, to predict a cryptocurrency's closing price. The LSTM is fed the close price, which is the price that the currency has at the end of the day, so it can learn from those values. The notebook creates two sets: a training set and a test set to assess the accuracy of the results. The data is then normalized using manual min-max scaling so that the model does not experience any bias; this also enhances the performance of the model. Then, the model is trained using three layers -- an LSTM, dropout, and dense layer-minimizing the loss through 50 epochs of training; from this training, a recurrent neural network (RNN) is produced and fitted to the training set. Additionally, a graph of the loss over each epoch is produced, with the loss minimizing over time. Finally, the notebook plots a line graph of the actual currency price in red and the predicted price in blue. The process is then repeated for several more cryptocurrencies to compare prediction models. The parameters for the LSTM, such as number of epochs and batch size, are tweaked to try and minimize the root mean square error.
Expressway visibility estimation based on image entropy and piecewise stationary time series analysis
Apr 08, 2018



Vision-based methods for visibility estimation can play a critical role in reducing traffic accidents caused by fog and haze. To overcome the disadvantages of current visibility estimation methods, we present a novel data-driven approach based on Gaussian image entropy and piecewise stationary time series analysis (SPEV). This is the first time that Gaussian image entropy is used for estimating atmospheric visibility. To lessen the impact of landscape and sunshine illuminance on visibility estimation, we used region of interest (ROI) analysis and took into account relative ratios of image entropy, to improve estimation accuracy. We assume fog and haze cause blurred images and that fog and haze can be considered as a piecewise stationary signal. We used piecewise stationary time series analysis to construct the piecewise causal relationship between image entropy and visibility. To obtain a real-world visibility measure during fog and haze, a subjective assessment was established through a study with 36 subjects who performed visibility observations. Finally, a total of two million videos were used for training the SPEV model and validate its effectiveness. The videos were collected from the constantly foggy and hazy Tongqi expressway in Jiangsu, China. The contrast model of visibility estimation was used for algorithm performance comparison, and the validation results of the SPEV model were encouraging as 99.14% of the relative errors were less than 10%.
Autoregressive models for biomedical signal processing
May 01, 2023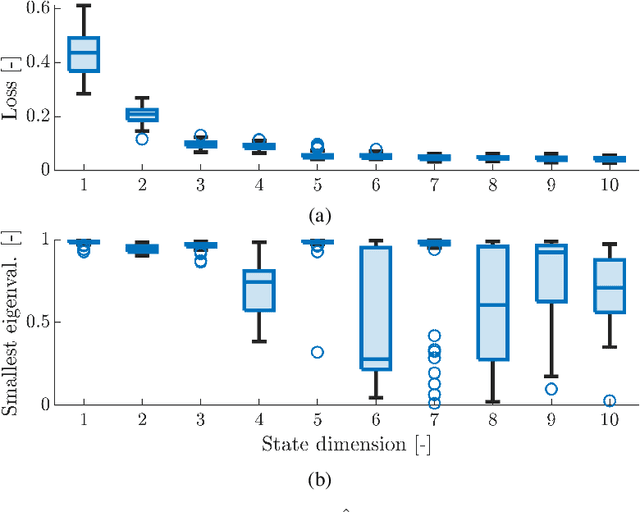
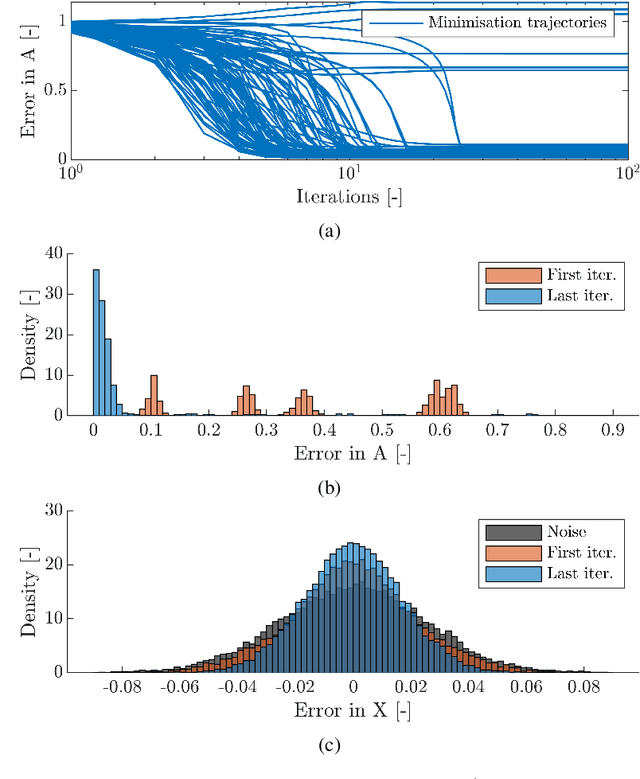
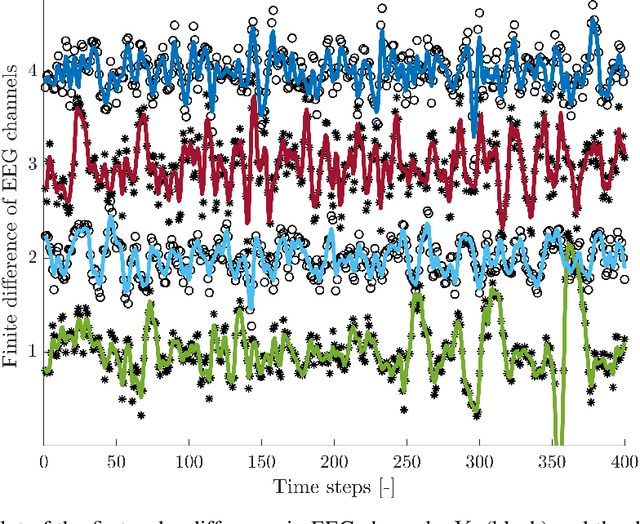
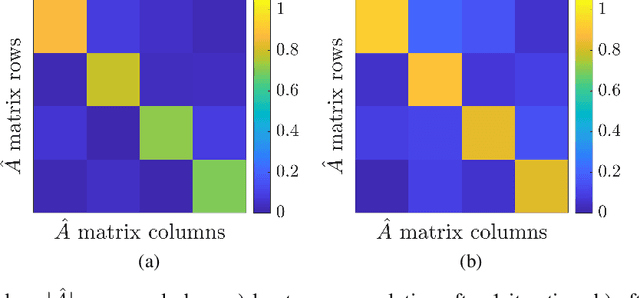
Autoregressive models are ubiquitous tools for the analysis of time series in many domains such as computational neuroscience and biomedical engineering. In these domains, data is, for example, collected from measurements of brain activity. Crucially, this data is subject to measurement errors as well as uncertainties in the underlying system model. As a result, standard signal processing using autoregressive model estimators may be biased. We present a framework for autoregressive modelling that incorporates these uncertainties explicitly via an overparameterised loss function. To optimise this loss, we derive an algorithm that alternates between state and parameter estimation. Our work shows that the procedure is able to successfully denoise time series and successfully reconstruct system parameters. This new paradigm can be used in a multitude of applications in neuroscience such as brain-computer interface data analysis and better understanding of brain dynamics in diseases such as epilepsy.
Kernel-based Joint Independence Tests for Multivariate Stationary and Nonstationary Time-Series
May 15, 2023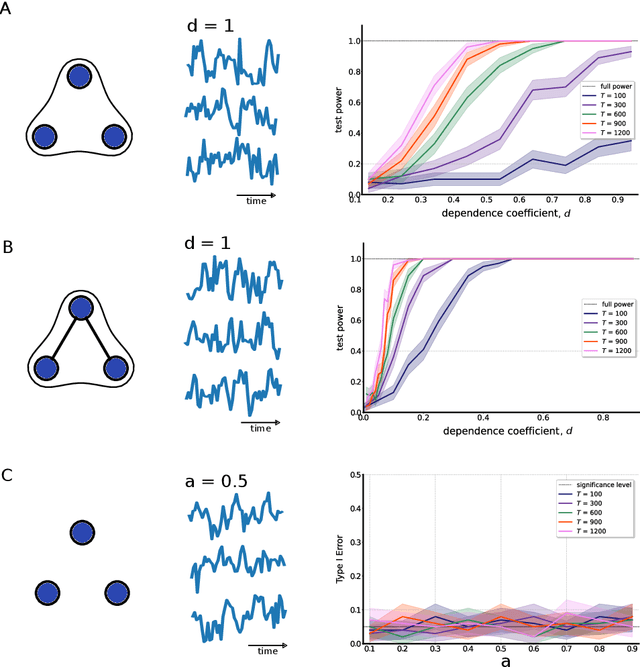

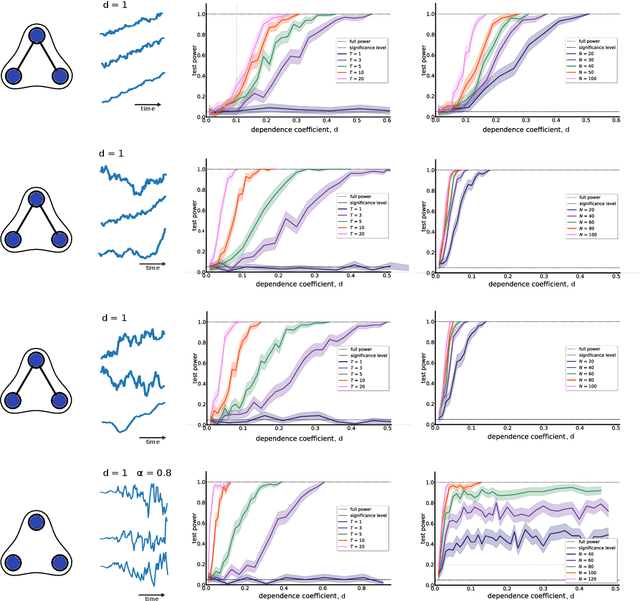
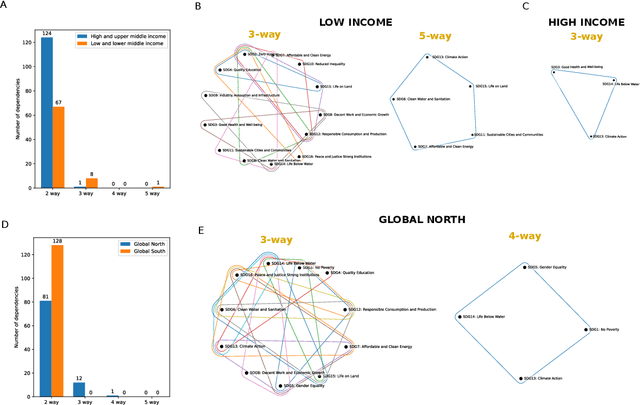
Multivariate time-series data that capture the temporal evolution of interconnected systems are ubiquitous in diverse areas. Understanding the complex relationships and potential dependencies among co-observed variables is crucial for the accurate statistical modelling and analysis of such systems. Here, we introduce kernel-based statistical tests of joint independence in multivariate time-series by extending the d-variable Hilbert-Schmidt independence criterion (dHSIC) to encompass both stationary and nonstationary random processes, thus allowing broader real-world applications. By leveraging resampling techniques tailored for both single- and multiple-realization time series, we show how the method robustly uncovers significant higher-order dependencies in synthetic examples, including frequency mixing data, as well as real-world climate and socioeconomic data. Our method adds to the mathematical toolbox for the analysis of complex high-dimensional time-series datasets.
5G Traffic Prediction with Time Series Analysis
Oct 07, 2021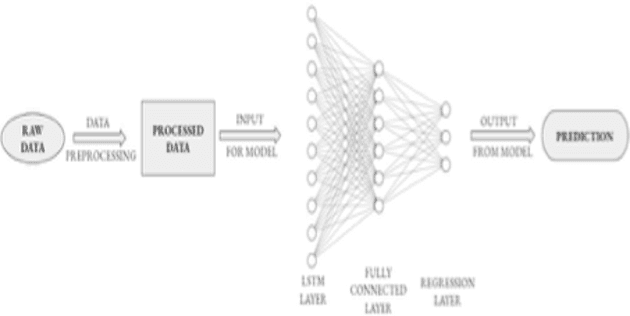
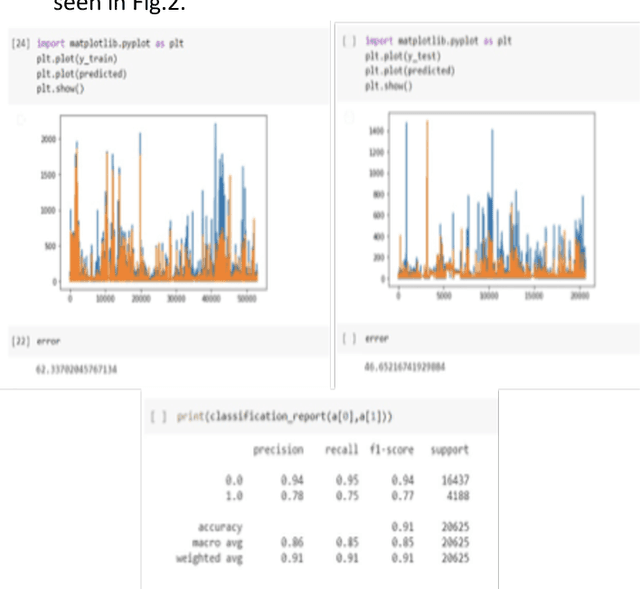
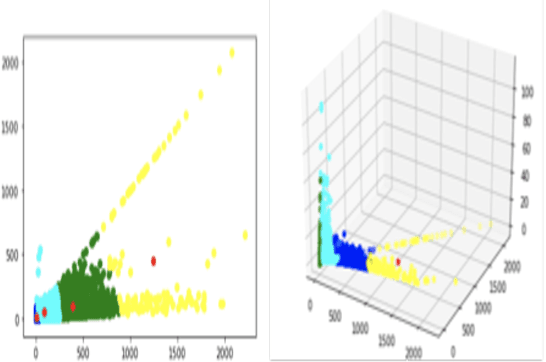
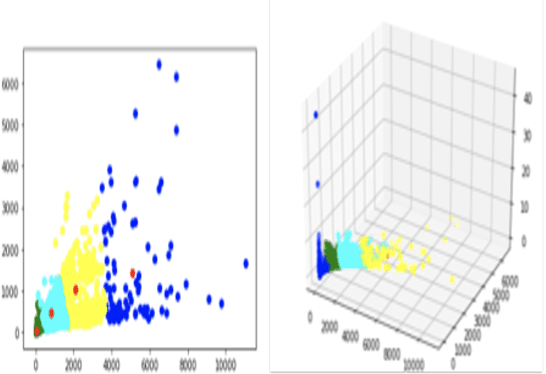
In todays day and age, a mobile phone has become a basic requirement needed for anyone to thrive. With the cellular traffic demand increasing so dramatically, it is now necessary to accurately predict the user traffic in cellular networks, so as to improve the performance in terms of resource allocation and utilisation. By leveraging the power of machine learning and identifying its usefulness in the field of cellular networks we try to achieve three main objectives classification of the application generating the traffic, prediction of packet arrival intensity and burst occurrence. The design of the prediction and classification system is done using Long Short Term Memory model. The LSTM predictor developed in this experiment would return the number of uplink packets and also estimate the probability of burst occurrence in the specified future time interval. For the purpose of classification, the regression layer in our LSTM prediction model is replaced by a softmax classifier which is used to classify the application generating the cellular traffic into one of the four applications including surfing, video calling, voice calling, and video streaming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge