Universally Elevating the Phase Transition Performance of Compressed Sensing: Non-Isometric Matrices are Not Necessarily Bad Matrices
Paper and Code
Jul 17, 2013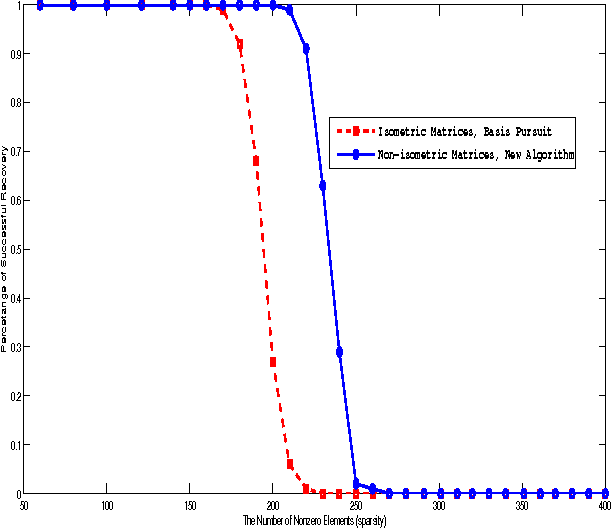
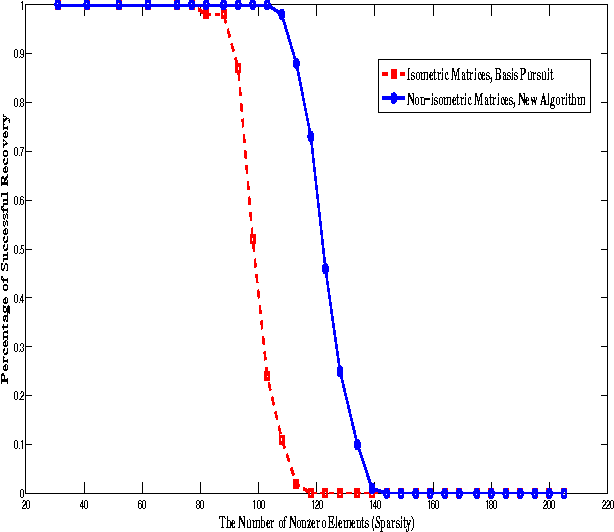
In compressed sensing problems, $\ell_1$ minimization or Basis Pursuit was known to have the best provable phase transition performance of recoverable sparsity among polynomial-time algorithms. It is of great theoretical and practical interest to find alternative polynomial-time algorithms which perform better than $\ell_1$ minimization. \cite{Icassp reweighted l_1}, \cite{Isit reweighted l_1}, \cite{XuScaingLaw} and \cite{iterativereweightedjournal} have shown that a two-stage re-weighted $\ell_1$ minimization algorithm can boost the phase transition performance for signals whose nonzero elements follow an amplitude probability density function (pdf) $f(\cdot)$ whose $t$-th derivative $f^{t}(0) \neq 0$ for some integer $t \geq 0$. However, for signals whose nonzero elements are strictly suspended from zero in distribution (for example, constant-modulus, only taking values `$+d$' or `$-d$' for some nonzero real number $d$), no polynomial-time signal recovery algorithms were known to provide better phase transition performance than plain $\ell_1$ minimization, especially for dense sensing matrices. In this paper, we show that a polynomial-time algorithm can universally elevate the phase-transition performance of compressed sensing, compared with $\ell_1$ minimization, even for signals with constant-modulus nonzero elements. Contrary to conventional wisdoms that compressed sensing matrices are desired to be isometric, we show that non-isometric matrices are not necessarily bad sensing matrices. In this paper, we also provide a framework for recovering sparse signals when sensing matrices are not isometric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge