Towards Practical Second-Order Optimizers in Deep Learning: Insights from Fisher Information Analysis
Paper and Code
Apr 26, 2025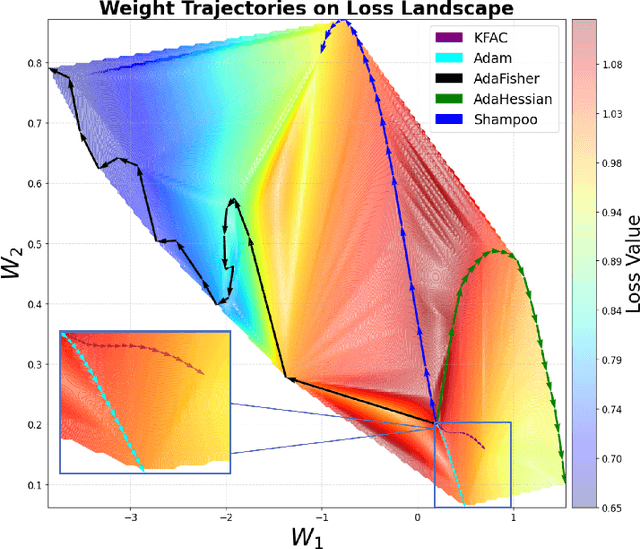

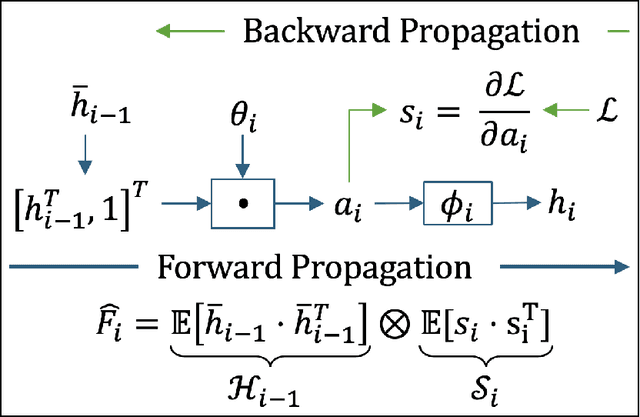
First-order optimization methods remain the standard for training deep neural networks (DNNs). Optimizers like Adam incorporate limited curvature information by preconditioning the stochastic gradient with a diagonal matrix. Despite the widespread adoption of first-order methods, second-order optimization algorithms often exhibit superior convergence compared to methods like Adam and SGD. However, their practicality in training DNNs is still limited by a significantly higher per-iteration computational cost compared to first-order methods. In this thesis, we present AdaFisher, a novel adaptive second-order optimizer that leverages a diagonal block-Kronecker approximation of the Fisher information matrix to adaptively precondition gradients. AdaFisher aims to bridge the gap between the improved convergence and generalization of second-order methods and the computational efficiency needed for training DNNs. Despite the traditionally slower speed of second-order optimizers, AdaFisher is effective for tasks such as image classification and language modeling, exhibiting remarkable stability and robustness during hyperparameter tuning. We demonstrate that AdaFisher outperforms state-of-the-art optimizers in both accuracy and convergence speed. The code is available from https://github.com/AtlasAnalyticsLab/AdaFisher.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge