The embedding dimension of Laplacian eigenfunction maps
Paper and Code
May 04, 2016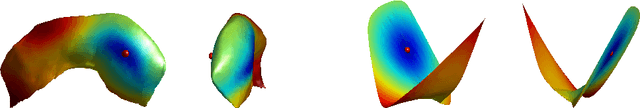

Any closed, connected Riemannian manifold $M$ can be smoothly embedded by its Laplacian eigenfunction maps into $\mathbb{R}^m$ for some $m$. We call the smallest such $m$ the maximal embedding dimension of $M$. We show that the maximal embedding dimension of $M$ is bounded from above by a constant depending only on the dimension of $M$, a lower bound for injectivity radius, a lower bound for Ricci curvature, and a volume bound. We interpret this result for the case of surfaces isometrically immersed in $\mathbb{R}^3$, showing that the maximal embedding dimension only depends on bounds for the Gaussian curvature, mean curvature, and surface area. Furthermore, we consider the relevance of these results for shape registration.
* Appl. Comput. Harmon. Anal. 37 (3) (2014) 516-530 * 16 pages, 2 figures, 3 theorems, and a torus in a pear tree
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge