Solving inverse problems using conditional invertible neural networks
Paper and Code
Jul 31, 2020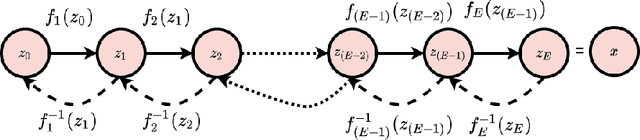
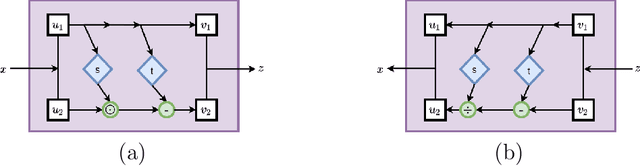
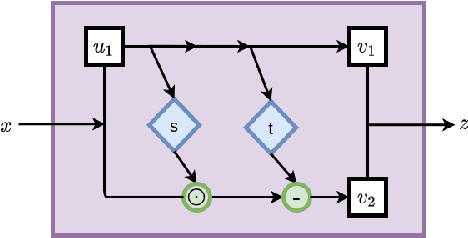
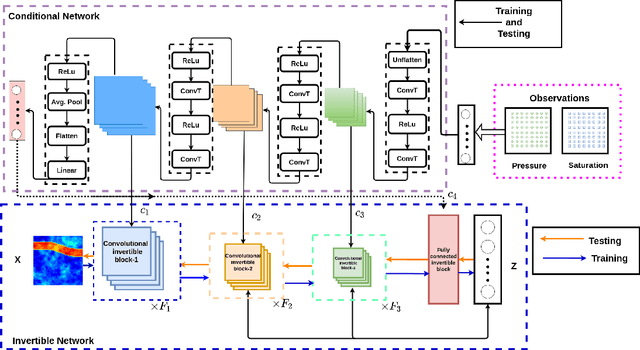
Inverse modeling for computing a high-dimensional spatially-varying property field from indirect sparse and noisy observations is a challenging problem. This is due to the complex physical system of interest often expressed in the form of multiscale PDEs, the high-dimensionality of the spatial property of interest, and the incomplete and noisy nature of observations. To address these challenges, we develop a model that maps the given observations to the unknown input field in the form of a surrogate model. This inverse surrogate model will then allow us to estimate the unknown input field for any given sparse and noisy output observations. Here, the inverse mapping is limited to a broad prior distribution of the input field with which the surrogate model is trained. In this work, we construct a two- and three-dimensional inverse surrogate models consisting of an invertible and a conditional neural network trained in an end-to-end fashion with limited training data. The invertible network is developed using a flow-based generative model. The developed inverse surrogate model is then applied for an inversion task of a multiphase flow problem where given the pressure and saturation observations the aim is to recover a high-dimensional non-Gaussian permeability field where the two facies consist of heterogeneous permeability and varying length-scales. For both the two- and three-dimensional surrogate models, the predicted sample realizations of the non-Gaussian permeability field are diverse with the predictive mean being close to the ground truth even when the model is trained with limited data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge