Risk and parameter convergence of logistic regression
Paper and Code
Jun 01, 2018
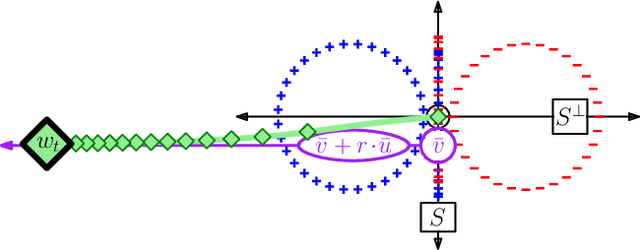
The logistic loss is strictly convex and does not attain its infimum; consequently the solutions of logistic regression are in general off at infinity. This work provides a convergence analysis of stochastic and batch gradient descent for logistic regression. Firstly, under the assumption of separability, stochastic gradient descent minimizes the population risk at rate $\mathcal{O}(\ln(t)^2/t)$ with high probability. Secondly, with or without separability, batch gradient descent minimizes the empirical risk at rate $\mathcal{O}(\ln(t)^2/t)$. Furthermore, parameter convergence can be characterized along a unique pair of complementary subspaces defined by the problem instance: one subspace along which strong convexity induces parameters to converge at rate $\mathcal{O}(\ln(t)^2/\sqrt{t})$, and its orthogonal complement along which separability induces parameters to converge in direction at rate $\mathcal{O}(\ln\ln(t) / \ln(t))$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge