Residual Tangent Kernels

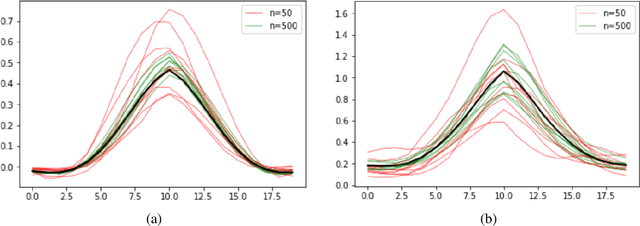
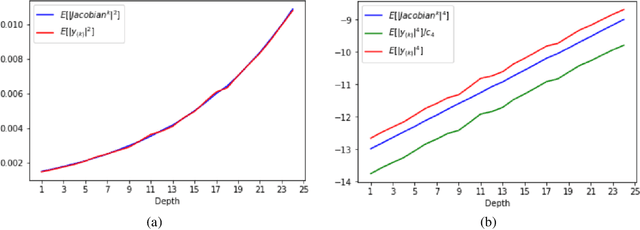
A recent body of work has focused on the theoretical study of neural networks at the regime of large width. Specifically, it was shown that training infinitely-wide and properly scaled vanilla ReLU networks using the L2 loss, is equivalent to kernel regression using the Neural Tangent Kernel (NTK), which is deterministic, and remains constant during training. In this work, we derive the form of the limiting kernel for architectures incorporating bypass connections, namely residual networks (ResNets), as well as to densely connected networks (DenseNets). In addition, we derive finite width and depth corrections for both cases. Our analysis reveals that deep practical residual architectures might operate much closer to the ``kernel regime'' than their vanilla counterparts: while in networks that do not use skip connections, convergence to the NTK requires one to fix depth, while increasing the layers' width. Our findings show that in ResNets, convergence to the NTK may occur when depth and width simultaneously tend to infinity, provided proper initialization. In DenseNets, however, convergence to the NTK as the width tend to infinity is guaranteed, at a rate that is independent of both depth and scale of the weights.