Quantum Embedding Search for Quantum Machine Learning

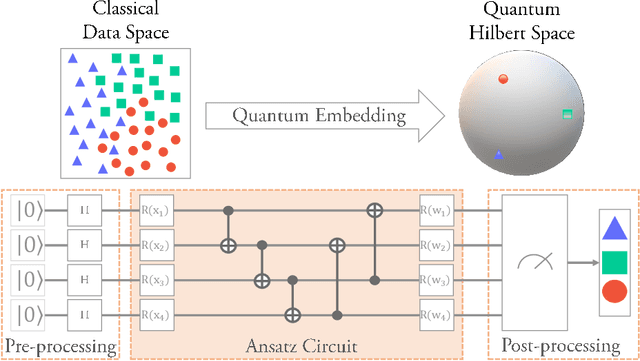
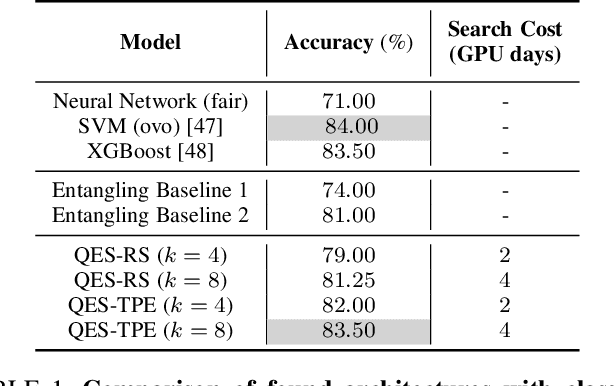
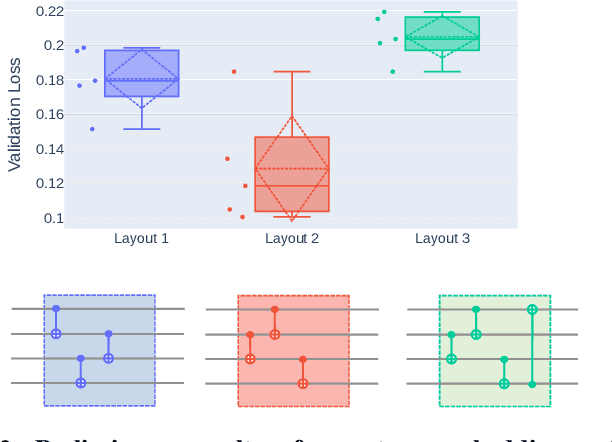
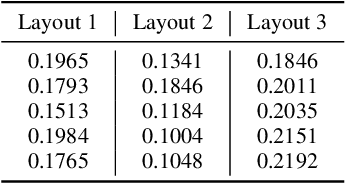
This paper introduces a novel quantum embedding search algorithm (QES, pronounced as "quest"), enabling search for optimal quantum embedding design for a specific dataset of interest. First, we establish the connection between the structures of quantum embedding and the representations of directed multi-graphs, enabling a well-defined search space. Second, we instigate the entanglement level to reduce the cardinality of the search space to a feasible size for practical implementations. Finally, we mitigate the cost of evaluating the true loss function by using surrogate models via sequential model-based optimization. We demonstrate the feasibility of our proposed approach on synthesis and Iris datasets, which empirically shows that found quantum embedding architecture by QES outperforms manual designs whereas achieving comparable performance to classical machine learning models.