PDE-constrained Models with Neural Network Terms: Optimization and Global Convergence
Paper and Code
May 18, 2021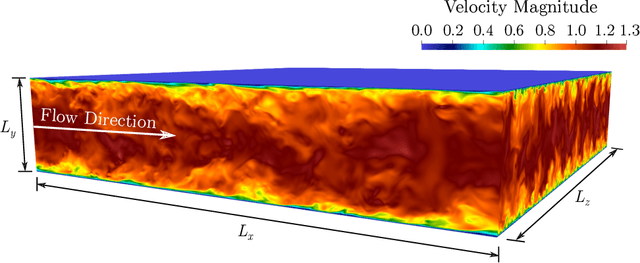
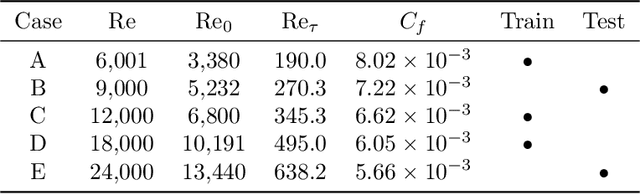
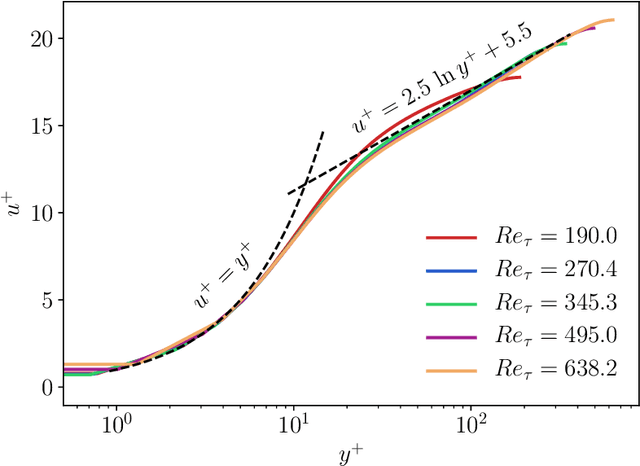

Recent research has used deep learning to develop partial differential equation (PDE) models in science and engineering. The functional form of the PDE is determined by a neural network, and the neural network parameters are calibrated to available data. Calibration of the embedded neural network can be performed by optimizing over the PDE. Motivated by these applications, we rigorously study the optimization of a class of linear elliptic PDEs with neural network terms. The neural network parameters in the PDE are optimized using gradient descent, where the gradient is evaluated using an adjoint PDE. As the number of parameters become large, the PDE and adjoint PDE converge to a non-local PDE system. Using this limit PDE system, we are able to prove convergence of the neural network-PDE to a global minimum during the optimization. The limit PDE system contains a non-local linear operator whose eigenvalues are positive but become arbitrarily small. The lack of a spectral gap for the eigenvalues poses the main challenge for the global convergence proof. Careful analysis of the spectral decomposition of the coupled PDE and adjoint PDE system is required. Finally, we use this adjoint method to train a neural network model for an application in fluid mechanics, in which the neural network functions as a closure model for the Reynolds-averaged Navier-Stokes (RANS) equations. The RANS neural network model is trained on several datasets for turbulent channel flow and is evaluated out-of-sample at different Reynolds numbers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge