On Uniformly Scaling Flows: A Density-Aligned Approach to Deep One-Class Classification
Paper and Code
Oct 10, 2025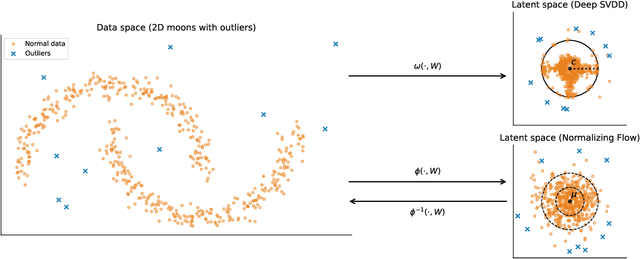
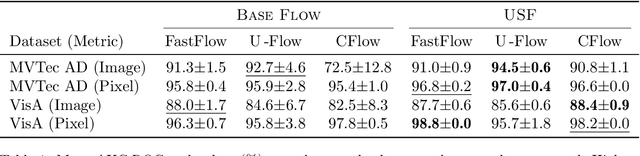
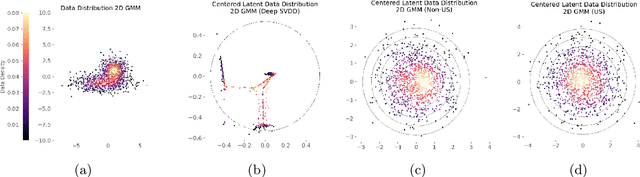
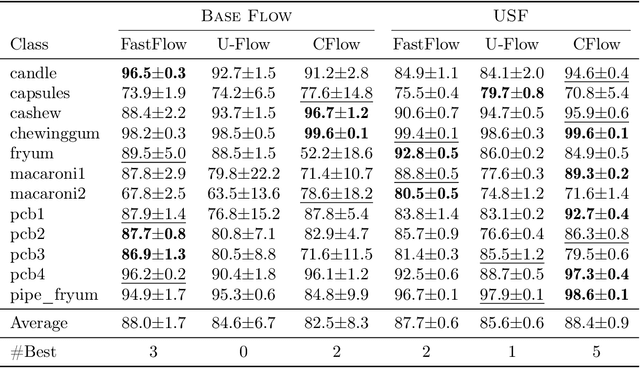
Unsupervised anomaly detection is often framed around two widely studied paradigms. Deep one-class classification, exemplified by Deep SVDD, learns compact latent representations of normality, while density estimators realized by normalizing flows directly model the likelihood of nominal data. In this work, we show that uniformly scaling flows (USFs), normalizing flows with a constant Jacobian determinant, precisely connect these approaches. Specifically, we prove how training a USF via maximum-likelihood reduces to a Deep SVDD objective with a unique regularization that inherently prevents representational collapse. This theoretical bridge implies that USFs inherit both the density faithfulness of flows and the distance-based reasoning of one-class methods. We further demonstrate that USFs induce a tighter alignment between negative log-likelihood and latent norm than either Deep SVDD or non-USFs, and how recent hybrid approaches combining one-class objectives with VAEs can be naturally extended to USFs. Consequently, we advocate using USFs as a drop-in replacement for non-USFs in modern anomaly detection architectures. Empirically, this substitution yields consistent performance gains and substantially improved training stability across multiple benchmarks and model backbones for both image-level and pixel-level detection. These results unify two major anomaly detection paradigms, advancing both theoretical understanding and practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge