On the Computation of PSNR for a Set of Images or Video
Paper and Code
Apr 30, 2021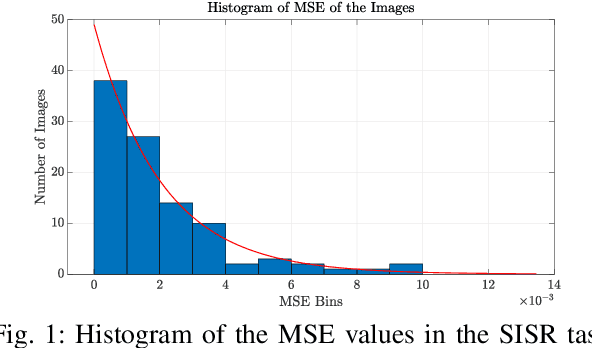
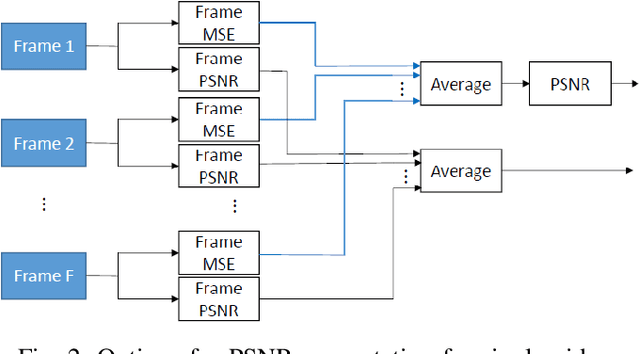
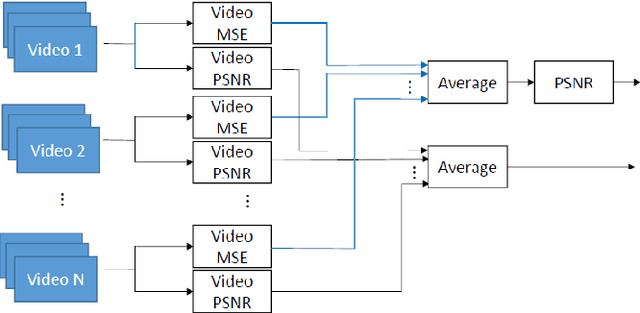
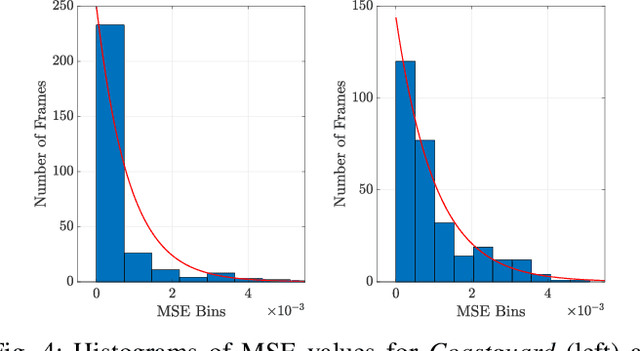
When comparing learned image/video restoration and compression methods, it is common to report peak-signal to noise ratio (PSNR) results. However, there does not exist a generally agreed upon practice to compute PSNR for sets of images or video. Some authors report average of individual image/frame PSNR, which is equivalent to computing a single PSNR from the geometric mean of individual image/frame mean-square error (MSE). Others compute a single PSNR from the arithmetic mean of frame MSEs for each video. Furthermore, some compute the MSE/PSNR of Y-channel only, while others compute MSE/PSNR for RGB channels. This paper investigates different approaches to computing PSNR for sets of images, single video, and sets of video and the relation between them. We show the difference between computing the PSNR based on arithmetic vs. geometric mean of MSE depends on the distribution of MSE over the set of images or video, and that this distribution is task-dependent. In particular, these two methods yield larger differences in restoration problems, where the MSE is exponentially distributed and smaller differences in compression problems, where the MSE distribution is narrower. We hope this paper will motivate the community to clearly describe how they compute reported PSNR values to enable consistent comparison.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge