On stochastic stabilization via non-smooth control Lyapunov functions
Paper and Code
May 26, 2022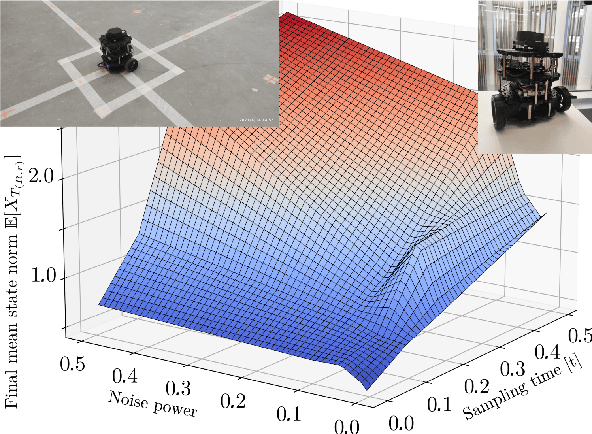
Control Lyapunov function is a central tool in stabilization. It generalizes an abstract energy function -- a Lyapunov function -- to the case of controlled systems. It is a known fact that most control Lyapunov functions are non-smooth -- so is the case in non-holonomic systems, like wheeled robots and cars. Frameworks for stabilization using non-smooth control Lyapunov functions exist, like Dini aiming and steepest descent. This work generalizes the related results to the stochastic case. As the groundwork, sampled control scheme is chosen in which control actions are computed at discrete moments in time using discrete measurements of the system state. In such a setup, special attention should be paid to the sample-to-sample behavior of the control Lyapunov function. A particular challenge here is a random noise acting on the system. The central result of this work is a theorem that states, roughly, that if there is a, generally non-smooth, control Lyapunov function, the given stochastic dynamical system can be practically stabilized in the sample-and-hold mode meaning that the control actions are held constant within sampling time steps. A particular control method chosen is based on Moreau-Yosida regularization, in other words, inf-convolution of the control Lyapunov function, but the overall framework is extendable to further control schemes. It is assumed that the system noise be bounded almost surely, although the case of unbounded noise is briefly addressed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge