Neural networks and rational functions
Paper and Code
Jun 11, 2017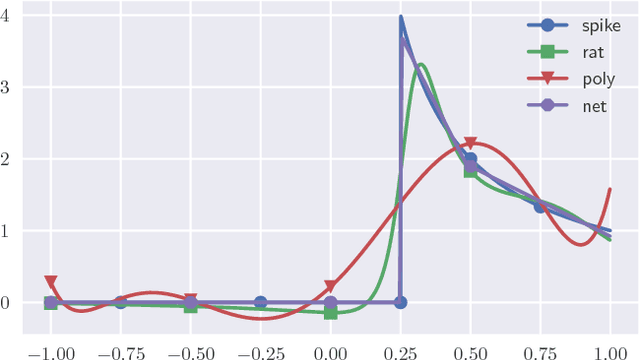
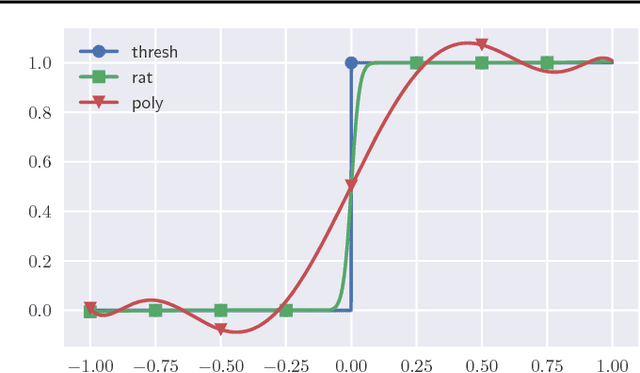
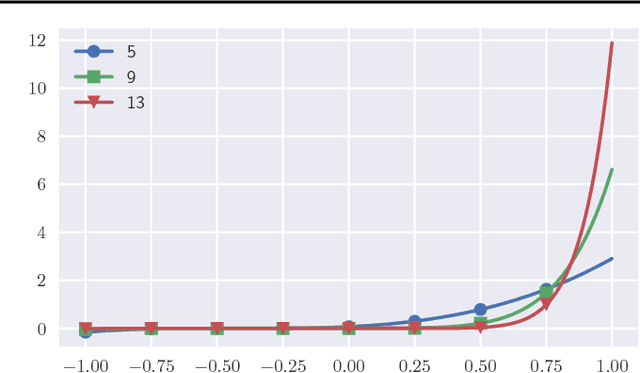
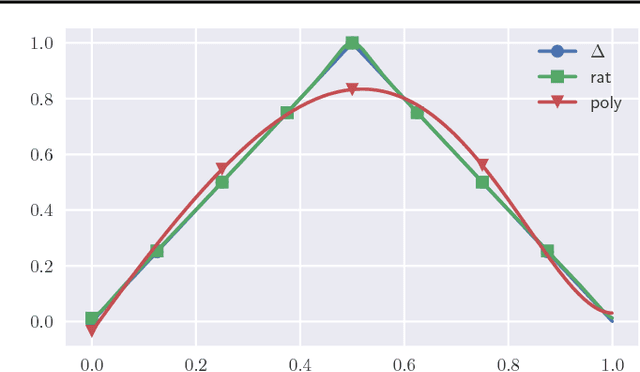
Neural networks and rational functions efficiently approximate each other. In more detail, it is shown here that for any ReLU network, there exists a rational function of degree $O(\text{polylog}(1/\epsilon))$ which is $\epsilon$-close, and similarly for any rational function there exists a ReLU network of size $O(\text{polylog}(1/\epsilon))$ which is $\epsilon$-close. By contrast, polynomials need degree $\Omega(\text{poly}(1/\epsilon))$ to approximate even a single ReLU. When converting a ReLU network to a rational function as above, the hidden constants depend exponentially on the number of layers, which is shown to be tight; in other words, a compositional representation can be beneficial even for rational functions.
* To appear, ICML 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge