Neural Network Layer Algebra: A Framework to Measure Capacity and Compression in Deep Learning
Paper and Code
Jul 02, 2021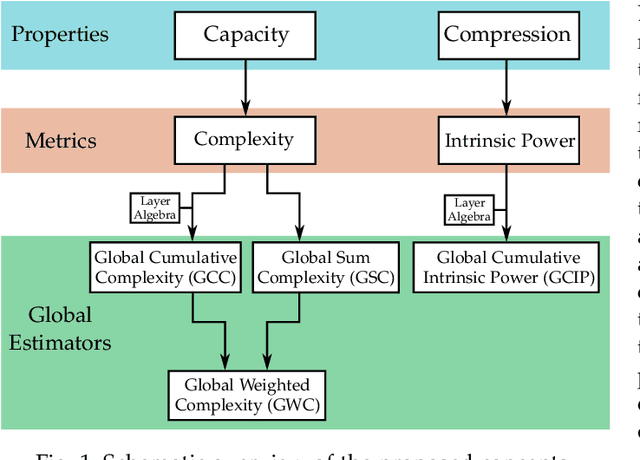
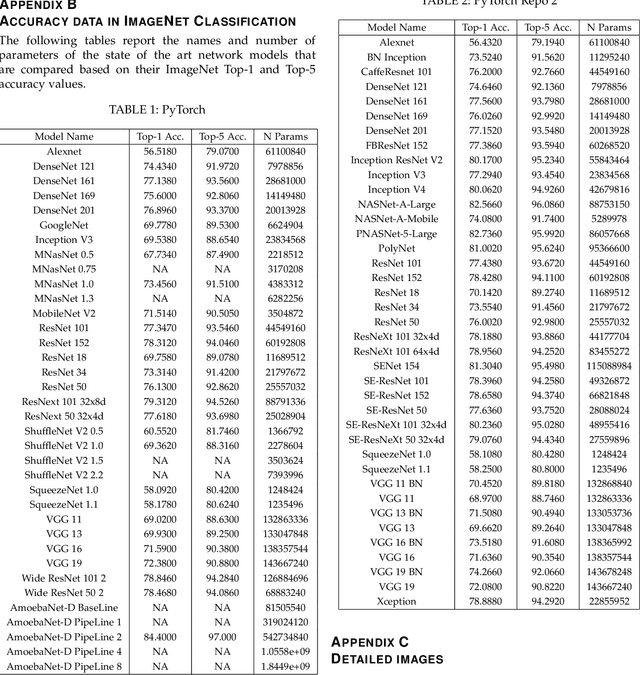
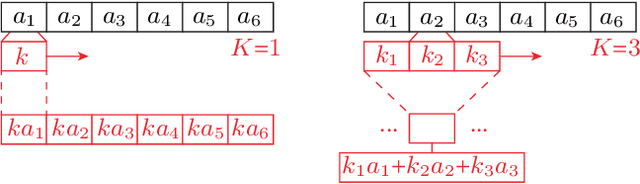
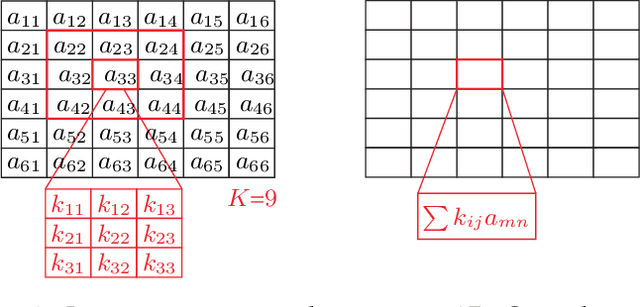
We present a new framework to measure the intrinsic properties of (deep) neural networks. While we focus on convolutional networks, our framework can be extrapolated to any network architecture. In particular, we evaluate two network properties, namely, capacity (related to expressivity) and compression, both of which depend only on the network structure and are independent of the training and test data. To this end, we propose two metrics: the first one, called layer complexity, captures the architectural complexity of any network layer; and, the second one, called layer intrinsic power, encodes how data is compressed along the network. The metrics are based on the concept of layer algebra, which is also introduced in this paper. This concept is based on the idea that the global properties depend on the network topology, and the leaf nodes of any neural network can be approximated using local transfer functions, thereby, allowing a simple computation of the global metrics. We also compare the properties of the state-of-the art architectures using our metrics and use the properties to analyze the classification accuracy on benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge