Minimum Wasserstein Distance Estimator under Finite Location-scale Mixtures
Paper and Code
Jul 03, 2021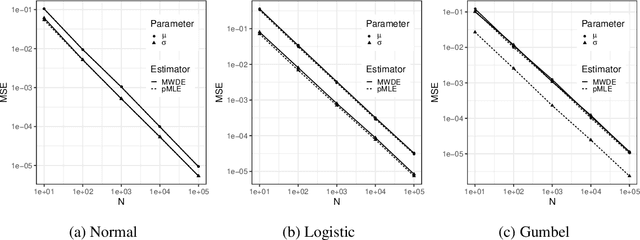
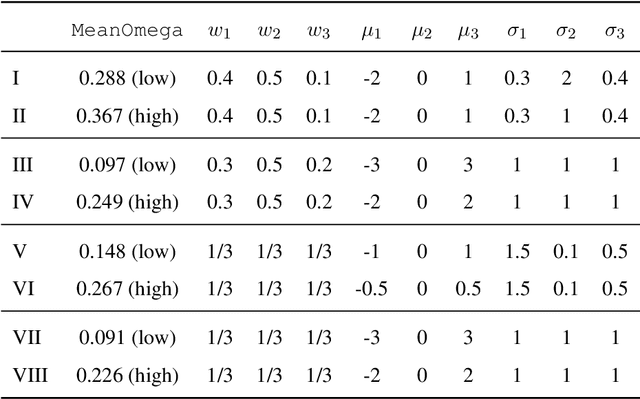
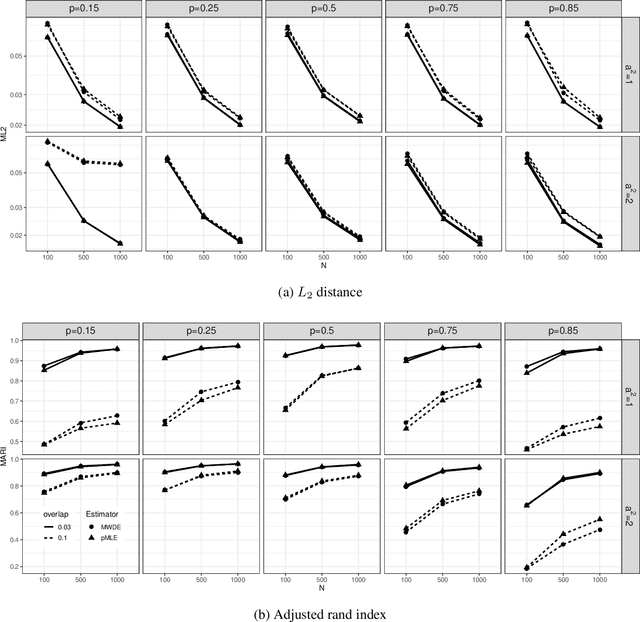
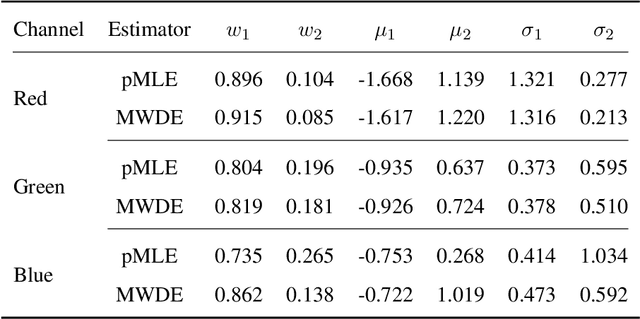
When a population exhibits heterogeneity, we often model it via a finite mixture: decompose it into several different but homogeneous subpopulations. Contemporary practice favors learning the mixtures by maximizing the likelihood for statistical efficiency and the convenient EM-algorithm for numerical computation. Yet the maximum likelihood estimate (MLE) is not well defined for the most widely used finite normal mixture in particular and for finite location-scale mixture in general. We hence investigate feasible alternatives to MLE such as minimum distance estimators. Recently, the Wasserstein distance has drawn increased attention in the machine learning community. It has intuitive geometric interpretation and is successfully employed in many new applications. Do we gain anything by learning finite location-scale mixtures via a minimum Wasserstein distance estimator (MWDE)? This paper investigates this possibility in several respects. We find that the MWDE is consistent and derive a numerical solution under finite location-scale mixtures. We study its robustness against outliers and mild model mis-specifications. Our moderate scaled simulation study shows the MWDE suffers some efficiency loss against a penalized version of MLE in general without noticeable gain in robustness. We reaffirm the general superiority of the likelihood based learning strategies even for the non-regular finite location-scale mixtures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge