Minimax Regret for Bandit Convex Optimisation of Ridge Functions
Paper and Code
Jun 06, 2021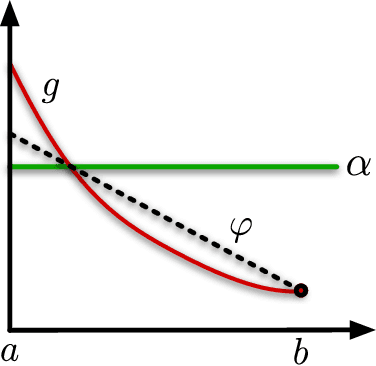
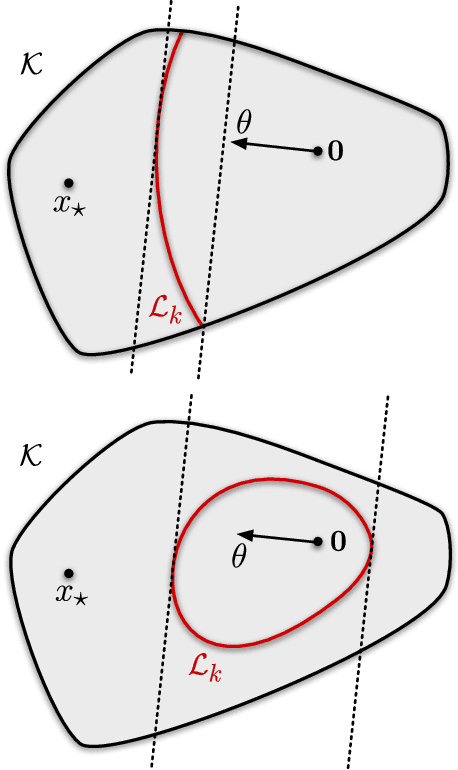
We analyse adversarial bandit convex optimisation with an adversary that is restricted to playing functions of the form $f_t(x) = g_t(\langle x, \theta\rangle)$ for convex $g_t : \mathbb R \to \mathbb R$ and unknown $\theta \in \mathbb R^d$ that is homogeneous over time. We provide a short information-theoretic proof that the minimax regret is at most $O(d \sqrt{n} \log(n \operatorname{diam}(\mathcal K)))$ where $n$ is the number of interactions, $d$ the dimension and $\operatorname{diam}(\mathcal K)$ is the diameter of the constraint set.
* Correcting an (instructive) error that leads to a weaker result
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge