Mean-Field Controllability and Decentralized Stabilization of Markov Chains, Part I: Global Controllability and Rational Feedbacks
Paper and Code
Mar 28, 2017
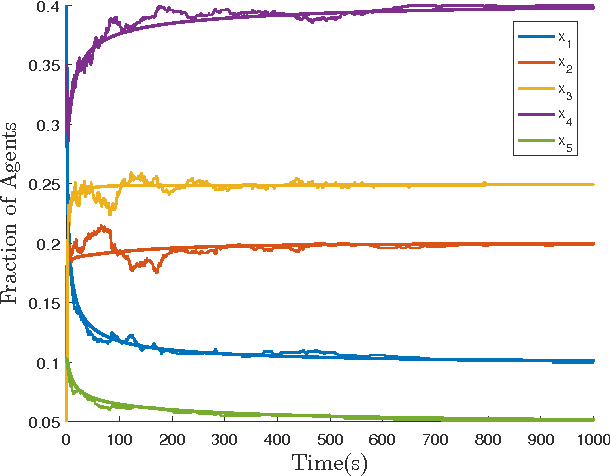
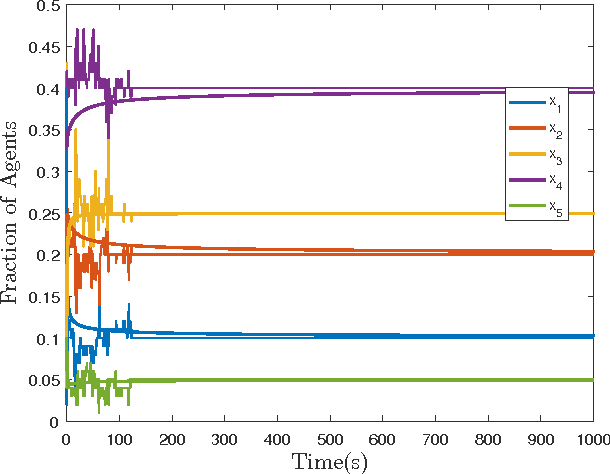
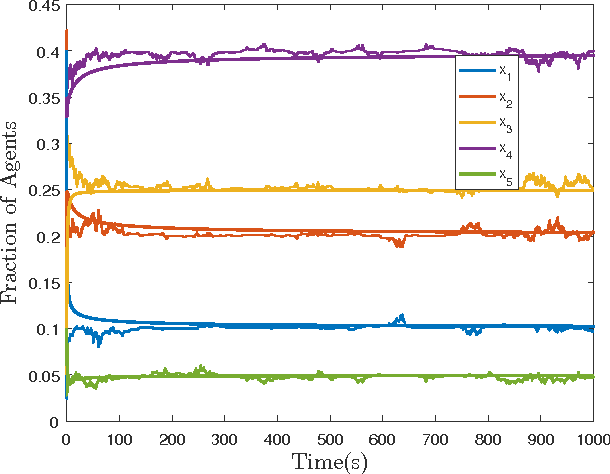
In this paper, we study the controllability and stabilizability properties of the Kolmogorov forward equation of a continuous time Markov chain (CTMC) evolving on a finite state space, using the transition rates as the control parameters. Firstly, we prove small-time local and global controllability from and to strictly positive equilibrium configurations when the underlying graph is strongly connected. Secondly, we show that there always exists a locally exponentially stabilizing decentralized linear (density-)feedback law that takes zero valu at equilibrium and respects the graph structure, provided that the transition rates are allowed to be negative and the desired target density lies in the interior of the set of probability densities. For bidirected graphs, that is, graphs where a directed edge in one direction implies an edge in the opposite direction, we show that this linear control law can be realized using a decentralized rational feedback law of the form k(x) = a(x) + b(x)f(x)/g(x) that also respects the graph structure and control constraints (positivity and zero at equilibrium). This enables the possibility of using Linear Matrix Inequality (LMI) based tools to algorithmically construct decentralized density feedback controllers for stabilization of a robotic swarm to a target task distribution with no task-switching at equilibrium, as we demonstrate with several numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge