Gradient Descent for Low-Rank Functions
Paper and Code
Jun 16, 2022
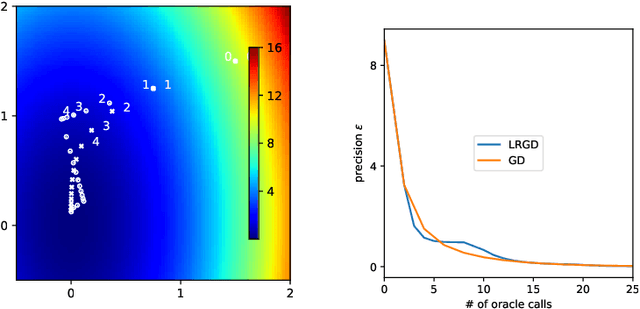
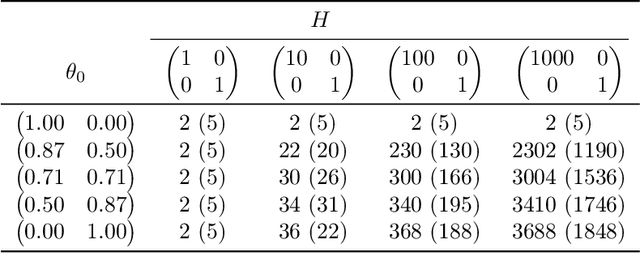
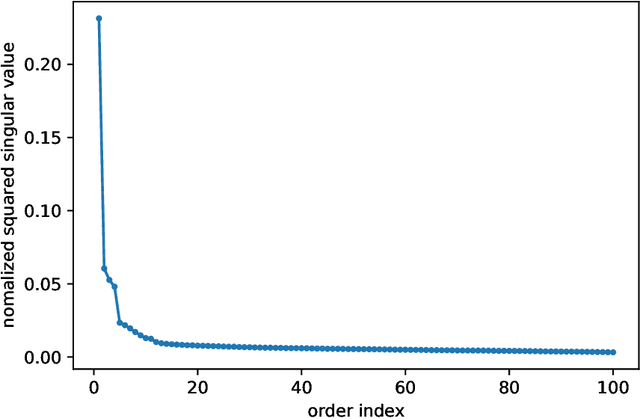
Several recent empirical studies demonstrate that important machine learning tasks, e.g., training deep neural networks, exhibit low-rank structure, where the loss function varies significantly in only a few directions of the input space. In this paper, we leverage such low-rank structure to reduce the high computational cost of canonical gradient-based methods such as gradient descent (GD). Our proposed \emph{Low-Rank Gradient Descent} (LRGD) algorithm finds an $\epsilon$-approximate stationary point of a $p$-dimensional function by first identifying $r \leq p$ significant directions, and then estimating the true $p$-dimensional gradient at every iteration by computing directional derivatives only along those $r$ directions. We establish that the "directional oracle complexities" of LRGD for strongly convex and non-convex objective functions are $\mathcal{O}(r \log(1/\epsilon) + rp)$ and $\mathcal{O}(r/\epsilon^2 + rp)$, respectively. When $r \ll p$, these complexities are smaller than the known complexities of $\mathcal{O}(p \log(1/\epsilon))$ and $\mathcal{O}(p/\epsilon^2)$ of {\gd} in the strongly convex and non-convex settings, respectively. Thus, LRGD significantly reduces the computational cost of gradient-based methods for sufficiently low-rank functions. In the course of our analysis, we also formally define and characterize the classes of exact and approximately low-rank functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge