Forward Looking Best-Response Multiplicative Weights Update Methods
Paper and Code
Jun 07, 2021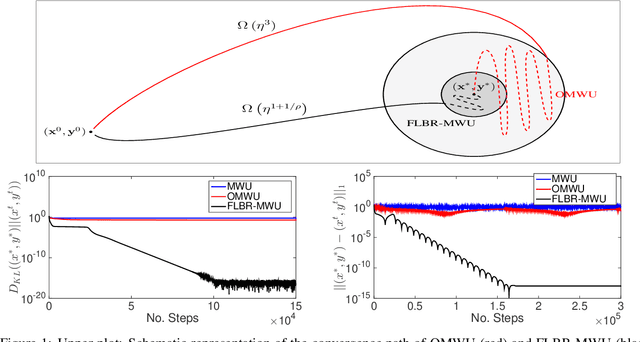

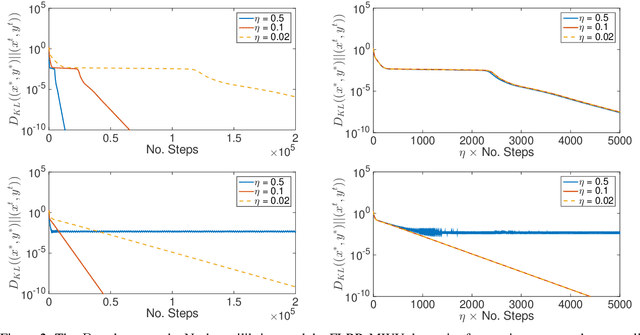
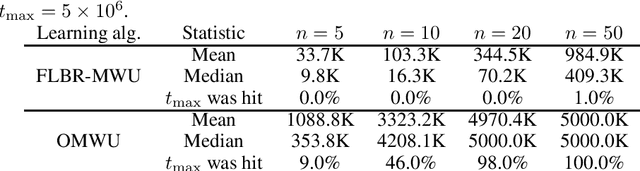
We propose a novel variant of the \emph{multiplicative weights update method} with forward-looking best-response strategies, that guarantees last-iterate convergence for \emph{zero-sum games} with a unique \emph{Nash equilibrium}. Particularly, we show that the proposed algorithm converges to an $\eta^{1/\rho}$-approximate Nash equilibrium, with $\rho > 1$, by decreasing the Kullback-Leibler divergence of each iterate by a rate of at least $\Omega(\eta^{1+\frac{1}{\rho}})$, for sufficiently small learning rate $\eta$. When our method enters a sufficiently small neighborhood of the solution, it becomes a contraction and converges to the Nash equilibrium of the game. Furthermore, we perform an experimental comparison with the recently proposed optimistic variant of the multiplicative weights update method, by \cite{Daskalakis2019LastIterateCZ}, which has also been proved to attain last-iterate convergence. Our findings reveal that our algorithm offers substantial gains both in terms of the convergence rate and the region of contraction relative to the previous approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge