Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical Systems
Paper and Code
Jul 09, 2025
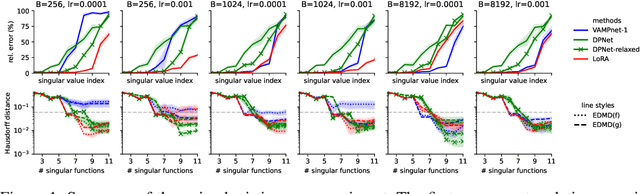
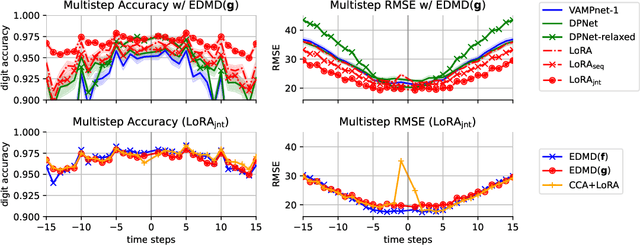
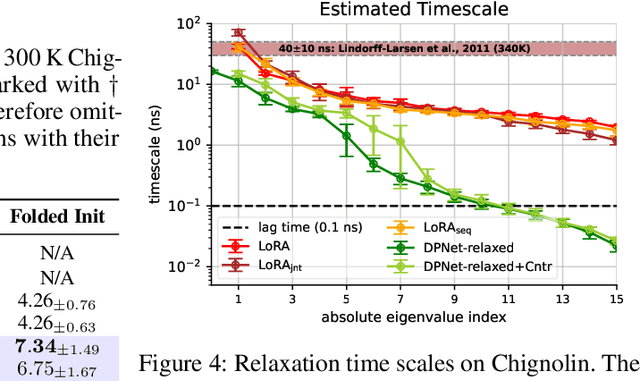
The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge