Efficient Parameter Estimation for Bayesian Network Classifiers using Hierarchical Linear Smoothing
Paper and Code
May 29, 2025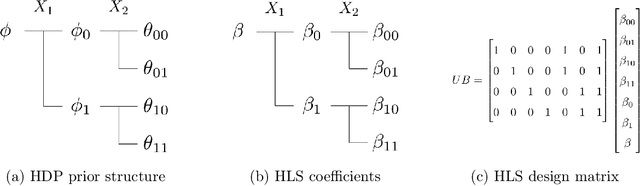

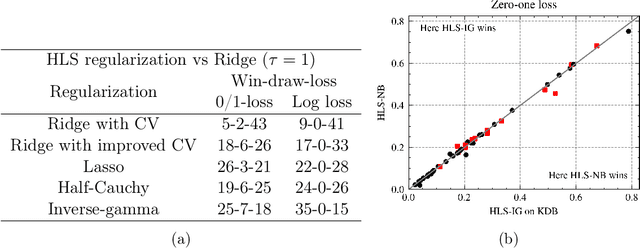
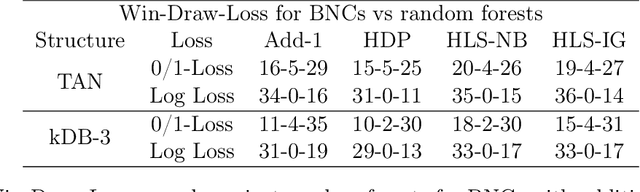
Bayesian network classifiers (BNCs) possess a number of properties desirable for a modern classifier: They are easily interpretable, highly scalable, and offer adaptable complexity. However, traditional methods for learning BNCs have historically underperformed when compared to leading classification methods such as random forests. Recent parameter smoothing techniques using hierarchical Dirichlet processes (HDPs) have enabled BNCs to achieve performance competitive with random forests on categorical data, but these techniques are relatively inflexible, and require a complicated, specialized sampling process. In this paper, we introduce a novel method for parameter estimation that uses a log-linear regression to approximate the behaviour of HDPs. As a linear model, our method is remarkably flexible and simple to interpret, and can leverage the vast literature on learning linear models. Our experiments show that our method can outperform HDP smoothing while being orders of magnitude faster, remaining competitive with random forests on categorical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge