Design of Data-Driven Mathematical Laws for Optimal Statistical Classification Systems

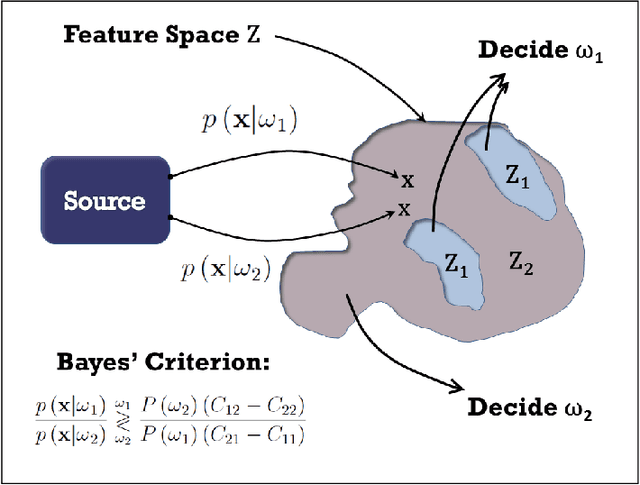
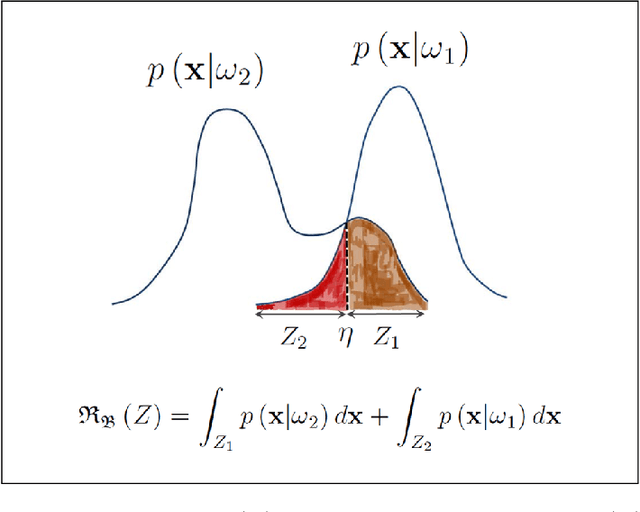
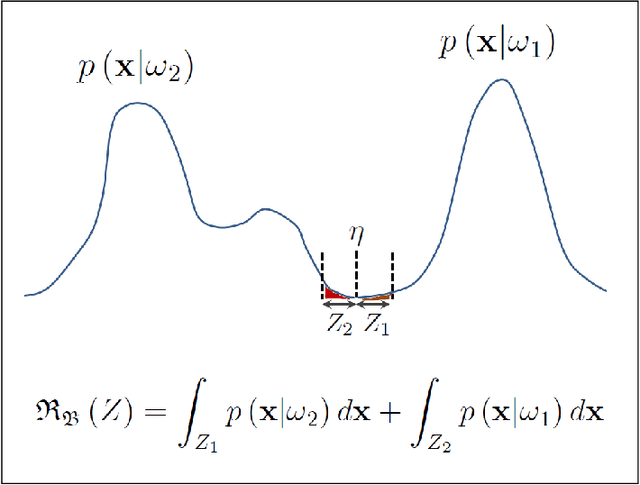
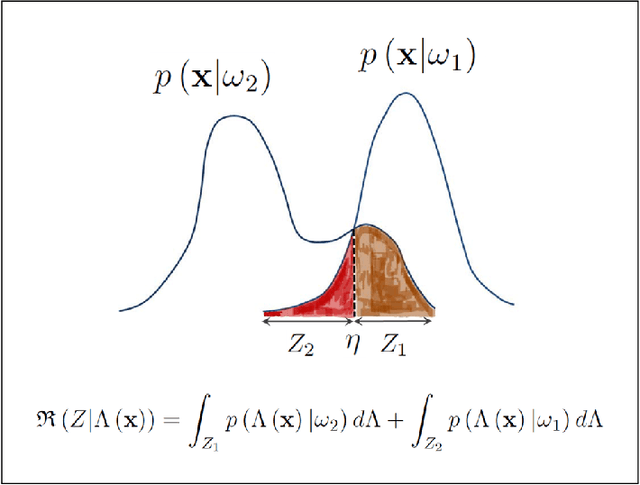
This article will devise data-driven, mathematical laws that generate optimal, statistical classification systems which achieve minimum error rates for data distributions with unchanging statistics. Thereby, I will design learning machines that minimize the expected risk or probability of misclassification. I will devise a system of fundamental equations of binary classification for a classification system in statistical equilibrium. I will use this system of equations to formulate the problem of learning unknown, linear and quadratic discriminant functions from data as a locus problem, thereby formulating geometric locus methods within a statistical framework. Solving locus problems involves finding equations of curves or surfaces defined by given properties and finding graphs or loci of given equations. I will devise three systems of data-driven, locus equations that generate optimal, statistical classification systems. Each class of learning machines satisfies fundamental statistical laws for a classification system in statistical equilibrium. Thereby, I will formulate three classes of learning machines that are scalable modules for optimal, statistical pattern recognition systems, all of which are capable of performing a wide variety of statistical pattern recognition tasks, where any given M-class statistical pattern recognition system exhibits optimal generalization performance for an M-class feature space.