Challenges and Pitfalls of Bayesian Unlearning
Paper and Code
Jul 07, 2022
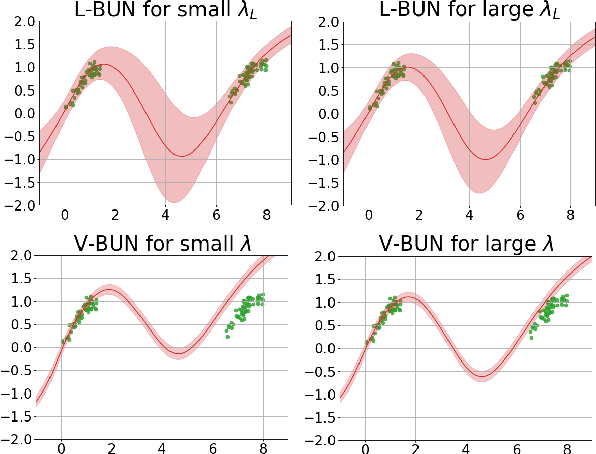
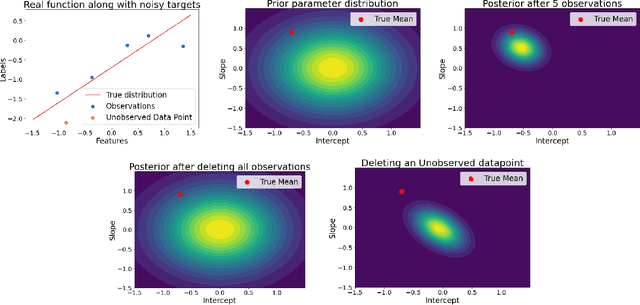
Machine unlearning refers to the task of removing a subset of training data, thereby removing its contributions to a trained model. Approximate unlearning are one class of methods for this task which avoid the need to retrain the model from scratch on the retained data. Bayes' rule can be used to cast approximate unlearning as an inference problem where the objective is to obtain the updated posterior by dividing out the likelihood of deleted data. However this has its own set of challenges as one often doesn't have access to the exact posterior of the model parameters. In this work we examine the use of the Laplace approximation and Variational Inference to obtain the updated posterior. With a neural network trained for a regression task as the guiding example, we draw insights on the applicability of Bayesian unlearning in practical scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge