Causal Inference on Multivariate and Mixed-Type Data
Paper and Code
Oct 16, 2017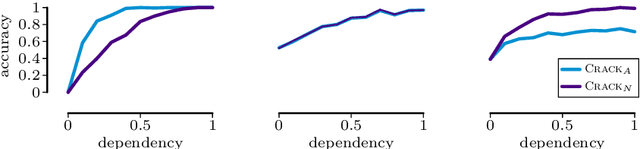
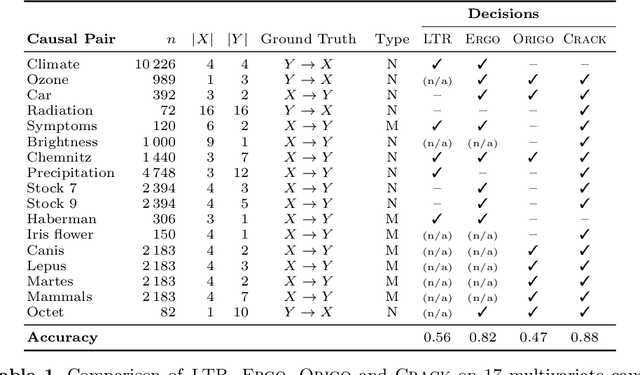
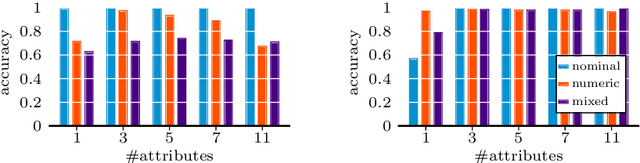
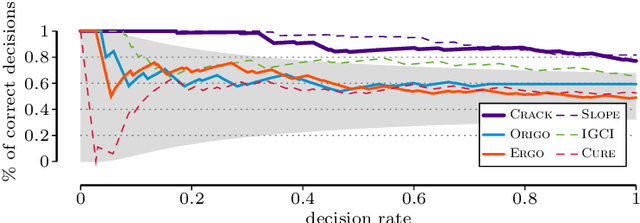
Given data over the joint distribution of two random variables $X$ and $Y$, we consider the problem of inferring the most likely causal direction between $X$ and $Y$. In particular, we consider the general case where both $X$ and $Y$ may be univariate or multivariate, and of the same or mixed data types. We take an information theoretic approach, based on Kolmogorov complexity, from which it follows that first describing the data over cause and then that of effect given cause is shorter than the reverse direction. The ideal score is not computable, but can be approximated through the Minimum Description Length (MDL) principle. Based on MDL, we propose two scores, one for when both $X$ and $Y$ are of the same single data type, and one for when they are mixed-type. We model dependencies between $X$ and $Y$ using classification and regression trees. As inferring the optimal model is NP-hard, we propose Crack, a fast greedy algorithm to determine the most likely causal direction directly from the data. Empirical evaluation on a wide range of data shows that Crack reliably, and with high accuracy, infers the correct causal direction on both univariate and multivariate cause-effect pairs over both single and mixed-type data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge