ButterflyFlow: Building Invertible Layers with Butterfly Matrices
Paper and Code
Sep 28, 2022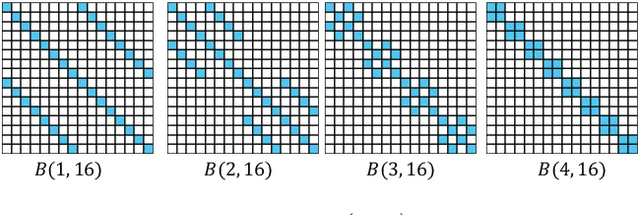
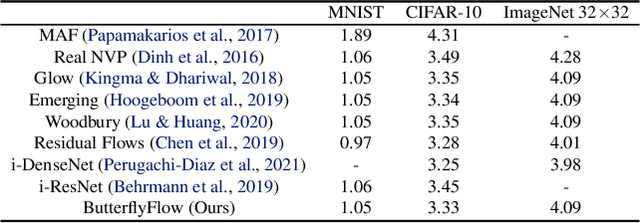
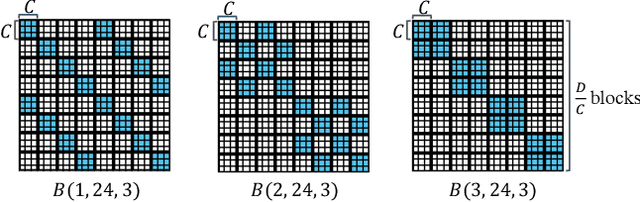

Normalizing flows model complex probability distributions using maps obtained by composing invertible layers. Special linear layers such as masked and 1x1 convolutions play a key role in existing architectures because they increase expressive power while having tractable Jacobians and inverses. We propose a new family of invertible linear layers based on butterfly layers, which are known to theoretically capture complex linear structures including permutations and periodicity, yet can be inverted efficiently. This representational power is a key advantage of our approach, as such structures are common in many real-world datasets. Based on our invertible butterfly layers, we construct a new class of normalizing flow models called ButterflyFlow. Empirically, we demonstrate that ButterflyFlows not only achieve strong density estimation results on natural images such as MNIST, CIFAR-10, and ImageNet 32x32, but also obtain significantly better log-likelihoods on structured datasets such as galaxy images and MIMIC-III patient cohorts -- all while being more efficient in terms of memory and computation than relevant baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge