Boltzmann Exploration Expectation-Maximisation
Paper and Code
Dec 18, 2019
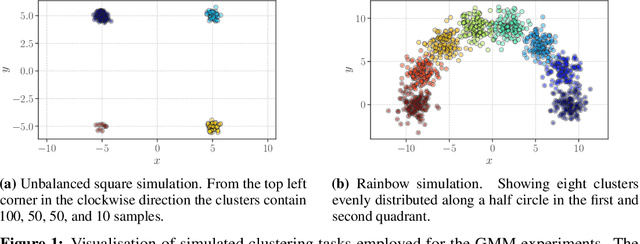

We present a general method for fitting finite mixture models (FMM). Learning in a mixture model consists of finding the most likely cluster assignment for each data-point, as well as finding the parameters of the clusters themselves. In many mixture models, this is difficult with current learning methods, where the most common approach is to employ monotone learning algorithms e.g. the conventional expectation-maximisation algorithm. While effective, the success of any monotone algorithm is crucially dependant on good parameter initialisation, where a common choice is $K$-means initialisation, commonly employed for Gaussian mixture models. For other types of mixture models, the path to good initialisation parameters is often unclear and may require a problem-specific solution. To this end, we propose a general heuristic learning algorithm that utilises Boltzmann exploration to assign each observation to a specific base distribution within the mixture model, which we call Boltzmann exploration expectation-maximisation (BEEM). With BEEM, hard assignments allow straight forward parameter learning for each base distribution by conditioning only on its assigned observations. Consequently, it can be applied to mixtures of any base distribution where single component parameter learning is tractable. The stochastic learning procedure is able to escape local optima and is thus insensitive to parameter initialisation. We show competitive performance on a number of synthetic benchmark cases as well as on real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge