Approximation Complexity of Maximum A Posteriori Inference in Sum-Product Networks
Paper and Code
Sep 05, 2017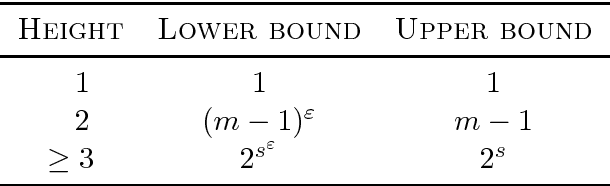
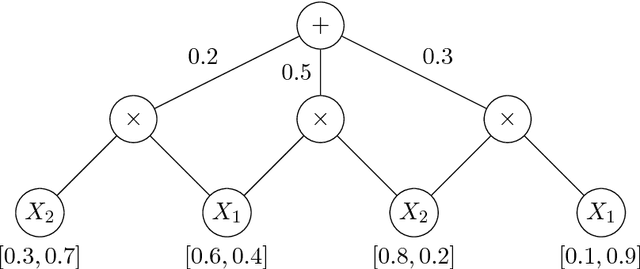
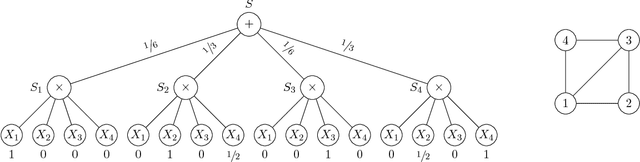
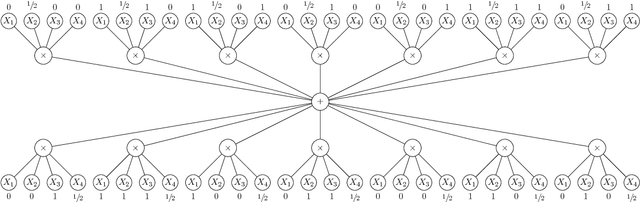
We discuss the computational complexity of approximating maximum a posteriori inference in sum-product networks. We first show NP-hardness in trees of height two by a reduction from maximum independent set; this implies non-approximability within a sublinear factor. We show that this is a tight bound, as we can find an approximation within a linear factor in networks of height two. We then show that, in trees of height three, it is NP-hard to approximate the problem within a factor $2^{f(n)}$ for any sublinear function $f$ of the size of the input $n$. Again, this bound is tight, as we prove that the usual max-product algorithm finds (in any network) approximations within factor $2^{c \cdot n}$ for some constant $c < 1$. Last, we present a simple algorithm, and show that it provably produces solutions at least as good as, and potentially much better than, the max-product algorithm. We empirically analyze the proposed algorithm against max-product using synthetic and realistic networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge