An Attract-Repel Decomposition of Undirected Networks

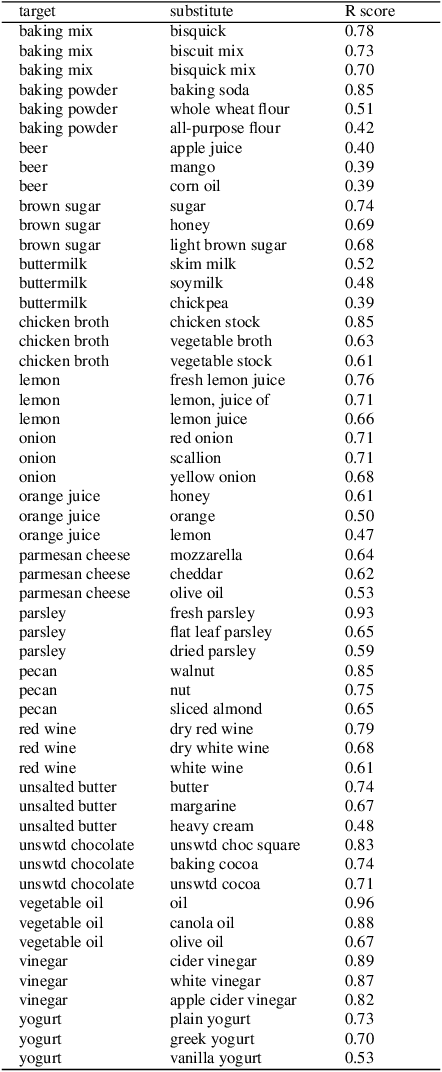
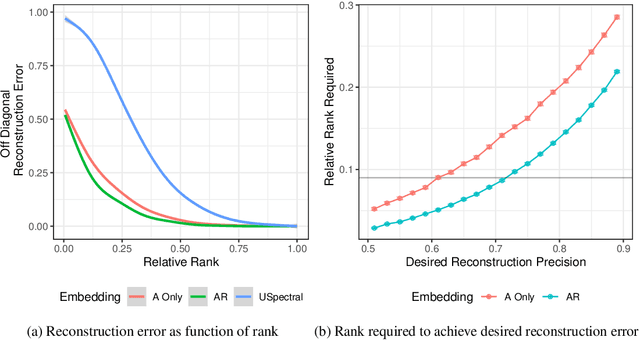
Dot product latent space embedding is a common form of representation learning in undirected graphs (e.g. social networks, co-occurrence networks). We show that such models have problems dealing with 'intransitive' situations where A is linked to B, B is linked to C but A is not linked to C. Such situations occur in social networks when opposites attract (heterophily) and in co-occurrence networks when there are substitute nodes (e.g. the presence of Pepsi or Coke, but rarely both, in otherwise similar purchase baskets). We present a simple expansion which we call the attract-repel (AR) decomposition: a set of latent attributes on which similar nodes attract and another set of latent attributes on which similar nodes repel. We demonstrate the AR decomposition in real social networks and show that it can be used to measure the amount of latent homophily and heterophily. In addition, it can be applied to co-occurrence networks to discover roles in teams and find substitutable ingredients in recipes.