AMP Chain Graphs: Minimal Separators and Structure Learning Algorithms

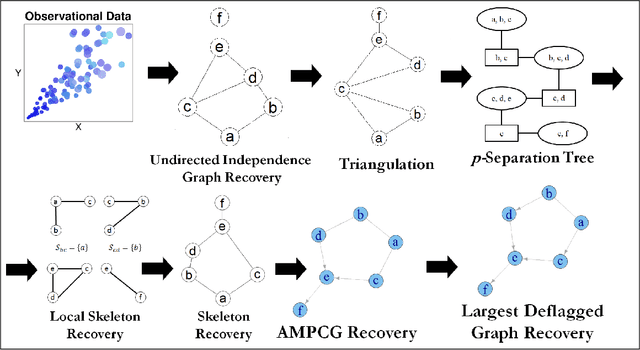
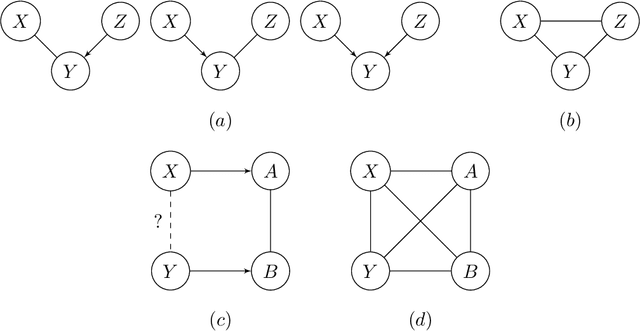
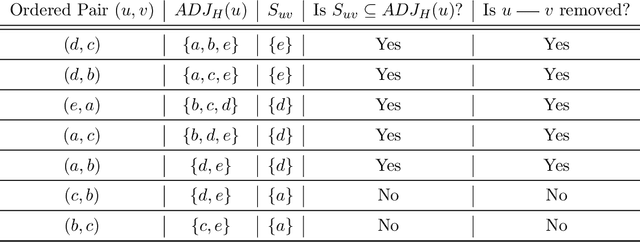
We address the problem of finding a minimal separator in an Andersson-Madigan-Perlman chain graph (AMP CG), namely, finding a set Z of nodes that separate a given non-adjacent pair of nodes such that no proper subset of Z separates that pair. We analyze several versions of this problem and offer polynomial-time algorithms for each. These include finding a minimal separator from a restricted set of nodes, finding a minimal separator for two given disjoint sets, and testing whether a given separator is minimal. We provide an extension of the decomposition approach for learning Bayesian networks (BNs) proposed by (Xie et. al.) to learn AMP CGs, which include BNs as a special case, under the faithfulness assumption and prove its correctness using the minimal separator results. The advantages of this decomposition approach hold in the more general setting: reduced complexity and increased power of computational independence tests. In addition, we show that the PC-like algorithm is order-dependent, in the sense that the output can depend on the order in which the variables are given. We propose two modifications of the PC-like algorithm that remove part or all of this order-dependence. Simulations under a variety of settings demonstrate the competitive performance of our decomposition-based method, called LCD-AMP, in comparison with the (modified version of) PC-like algorithm. In fact, the decomposition-based algorithm usually outperforms the PC-like algorithm. We empirically show that the results of both algorithms are more accurate and stable when the sample size is reasonably large and the underlying graph is sparse.