A Topological Approach to Spectral Clustering

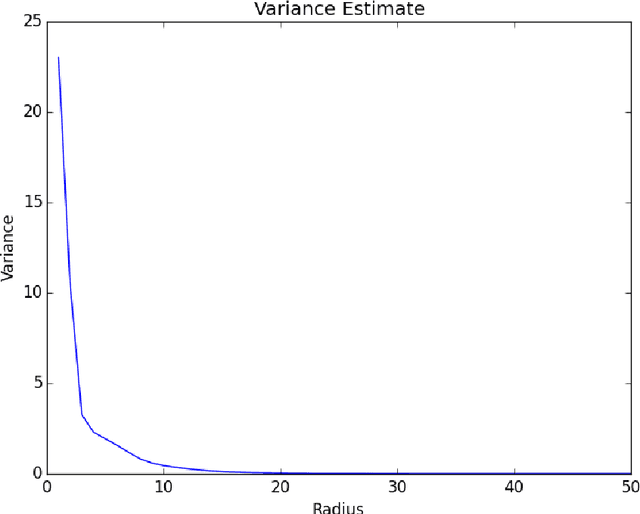
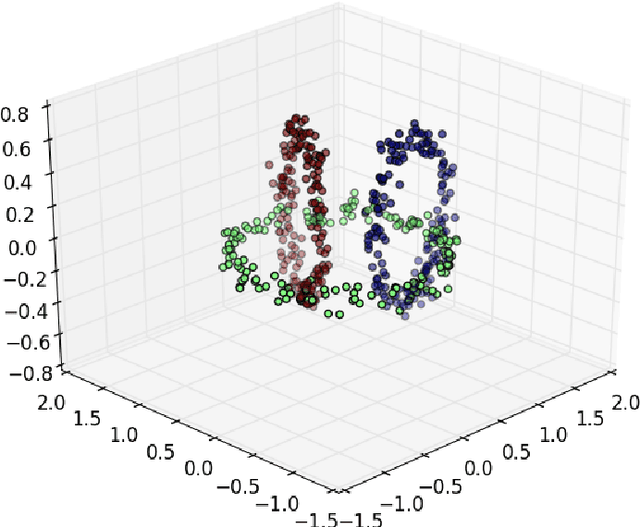
We propose a clustering algorithm which, for input, takes data assumed to be sampled from a uniform distribution supported on a metric space $X$, and outputs a clustering of the data based on a topological estimate of the connected components of $X$. The algorithm works by choosing a weighted graph on the samples from a natural one-parameter family of graphs using an error based on the heat operator on the graphs. The estimated connected components of $X$ are identified as the support of the eigenfunctions of the heat operator with eigenvalue $1$, which allows the algorithm to work without requiring the number of expected clusters as input.