A Central Limit Theorem for Differentially Private Query Answering
Paper and Code
Mar 15, 2021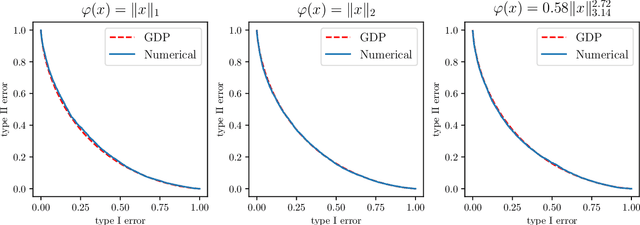
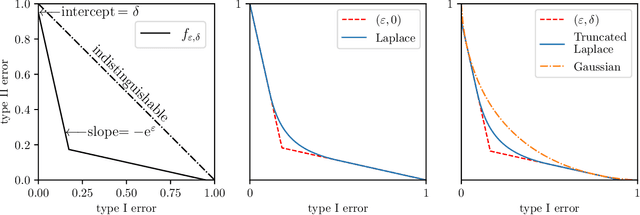

Perhaps the single most important use case for differential privacy is to privately answer numerical queries, which is usually achieved by adding noise to the answer vector. The central question, therefore, is to understand which noise distribution optimizes the privacy-accuracy trade-off, especially when the dimension of the answer vector is high. Accordingly, extensive literature has been dedicated to the question and the upper and lower bounds have been matched up to constant factors [BUV18, SU17]. In this paper, we take a novel approach to address this important optimality question. We first demonstrate an intriguing central limit theorem phenomenon in the high-dimensional regime. More precisely, we prove that a mechanism is approximately Gaussian Differentially Private [DRS21] if the added noise satisfies certain conditions. In particular, densities proportional to $\mathrm{e}^{-\|x\|_p^\alpha}$, where $\|x\|_p$ is the standard $\ell_p$-norm, satisfies the conditions. Taking this perspective, we make use of the Cramer--Rao inequality and show an "uncertainty principle"-style result: the product of the privacy parameter and the $\ell_2$-loss of the mechanism is lower bounded by the dimension. Furthermore, the Gaussian mechanism achieves the constant-sharp optimal privacy-accuracy trade-off among all such noises. Our findings are corroborated by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge