Anonymized Histograms in Intermediate Privacy Models

We study the problem of privately computing the anonymized histogram (a.k.a. unattributed histogram), which is defined as the histogram without item labels. Previous works have provided algorithms with $\ell_1$- and $\ell_2^2$-errors of $O_\varepsilon(\sqrt{n})$ in the central model of differential privacy (DP). In this work, we provide an algorithm with a nearly matching error guarantee of $\tilde{O}_\varepsilon(\sqrt{n})$ in the shuffle DP and pan-private models. Our algorithm is very simple: it just post-processes the discrete Laplace-noised histogram! Using this algorithm as a subroutine, we show applications in privately estimating symmetric properties of distributions such as entropy, support coverage, and support size.

Private Isotonic Regression

In this paper, we consider the problem of differentially private (DP) algorithms for isotonic regression. For the most general problem of isotonic regression over a partially ordered set (poset) $\mathcal{X}$ and for any Lipschitz loss function, we obtain a pure-DP algorithm that, given $n$ input points, has an expected excess empirical risk of roughly $\mathrm{width}(\mathcal{X}) \cdot \log|\mathcal{X}| / n$, where $\mathrm{width}(\mathcal{X})$ is the width of the poset. In contrast, we also obtain a near-matching lower bound of roughly $(\mathrm{width}(\mathcal{X}) + \log |\mathcal{X}|) / n$, that holds even for approximate-DP algorithms. Moreover, we show that the above bounds are essentially the best that can be obtained without utilizing any further structure of the poset. In the special case of a totally ordered set and for $\ell_1$ and $\ell_2^2$ losses, our algorithm can be implemented in near-linear running time; we also provide extensions of this algorithm to the problem of private isotonic regression with additional structural constraints on the output function.

Algorithms with More Granular Differential Privacy Guarantees

Differential privacy is often applied with a privacy parameter that is larger than the theory suggests is ideal; various informal justifications for tolerating large privacy parameters have been proposed. In this work, we consider partial differential privacy (DP), which allows quantifying the privacy guarantee on a per-attribute basis. In this framework, we study several basic data analysis and learning tasks, and design algorithms whose per-attribute privacy parameter is smaller that the best possible privacy parameter for the entire record of a person (i.e., all the attributes).

Cryptographic Hardness of Learning Halfspaces with Massart Noise

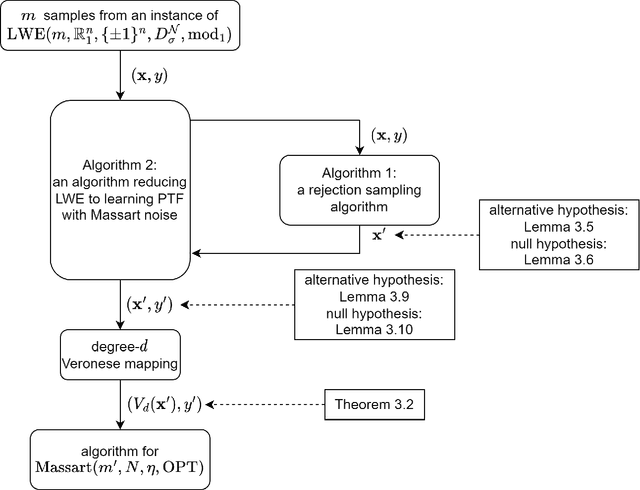
We study the complexity of PAC learning halfspaces in the presence of Massart noise. In this problem, we are given i.i.d. labeled examples $(\mathbf{x}, y) \in \mathbb{R}^N \times \{ \pm 1\}$, where the distribution of $\mathbf{x}$ is arbitrary and the label $y$ is a Massart corruption of $f(\mathbf{x})$, for an unknown halfspace $f: \mathbb{R}^N \to \{ \pm 1\}$, with flipping probability $\eta(\mathbf{x}) \leq \eta < 1/2$. The goal of the learner is to compute a hypothesis with small 0-1 error. Our main result is the first computational hardness result for this learning problem. Specifically, assuming the (widely believed) subexponential-time hardness of the Learning with Errors (LWE) problem, we show that no polynomial-time Massart halfspace learner can achieve error better than $\Omega(\eta)$, even if the optimal 0-1 error is small, namely $\mathrm{OPT} = 2^{-\log^{c} (N)}$ for any universal constant $c \in (0, 1)$. Prior work had provided qualitatively similar evidence of hardness in the Statistical Query model. Our computational hardness result essentially resolves the polynomial PAC learnability of Massart halfspaces, by showing that known efficient learning algorithms for the problem are nearly best possible.

Faster Privacy Accounting via Evolving Discretization

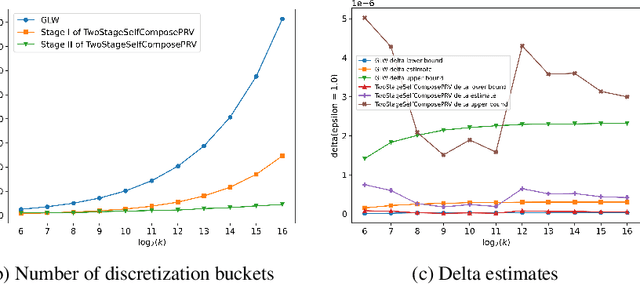
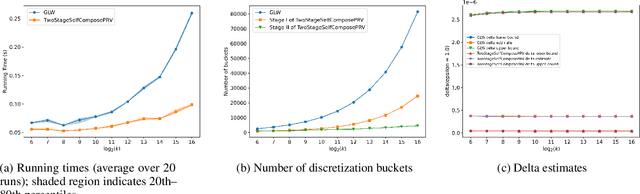
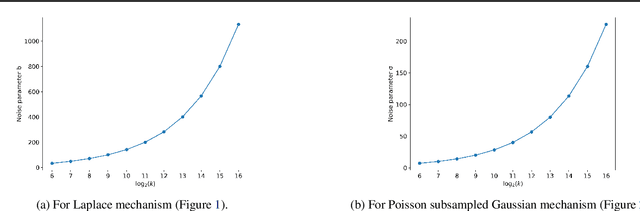
We introduce a new algorithm for numerical composition of privacy random variables, useful for computing the accurate differential privacy parameters for composition of mechanisms. Our algorithm achieves a running time and memory usage of $\mathrm{polylog}(k)$ for the task of self-composing a mechanism, from a broad class of mechanisms, $k$ times; this class, e.g., includes the sub-sampled Gaussian mechanism, that appears in the analysis of differentially private stochastic gradient descent. By comparison, recent work by Gopi et al. (NeurIPS 2021) has obtained a running time of $\widetilde{O}(\sqrt{k})$ for the same task. Our approach extends to the case of composing $k$ different mechanisms in the same class, improving upon their running time and memory usage from $\widetilde{O}(k^{1.5})$ to $\widetilde{O}(k)$.

Connect the Dots: Tighter Discrete Approximations of Privacy Loss Distributions

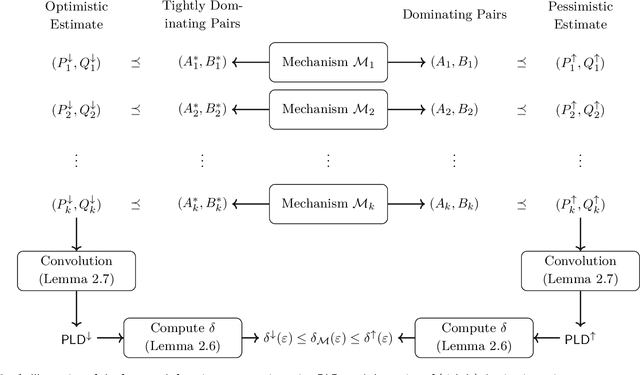
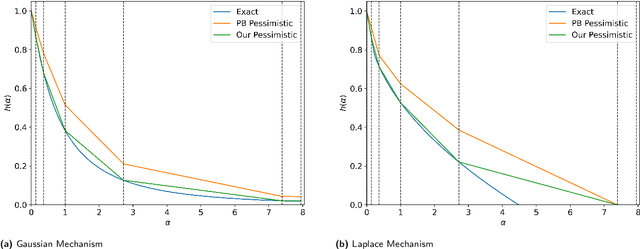
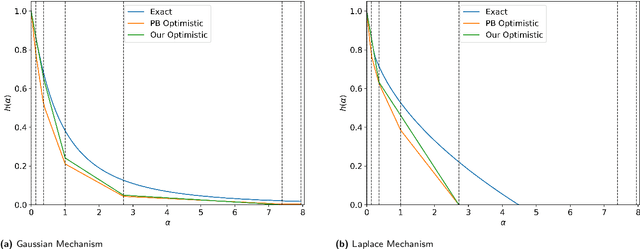
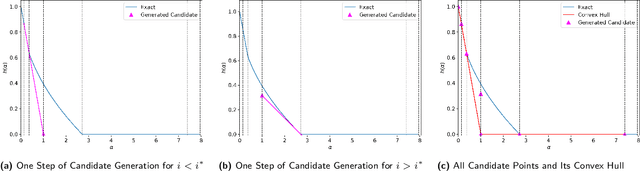
The privacy loss distribution (PLD) provides a tight characterization of the privacy loss of a mechanism in the context of differential privacy (DP). Recent work has shown that PLD-based accounting allows for tighter $(\varepsilon, \delta)$-DP guarantees for many popular mechanisms compared to other known methods. A key question in PLD-based accounting is how to approximate any (potentially continuous) PLD with a PLD over any specified discrete support. We present a novel approach to this problem. Our approach supports both pessimistic estimation, which overestimates the hockey-stick divergence (i.e., $\delta$) for any value of $\varepsilon$, and optimistic estimation, which underestimates the hockey-stick divergence. Moreover, we show that our pessimistic estimate is the best possible among all pessimistic estimates. Experimental evaluation shows that our approach can work with much larger discretization intervals while keeping a similar error bound compared to previous approaches and yet give a better approximation than existing methods.

Private Robust Estimation by Stabilizing Convex Relaxations

We give the first polynomial time and sample $(\epsilon, \delta)$-differentially private (DP) algorithm to estimate the mean, covariance and higher moments in the presence of a constant fraction of adversarial outliers. Our algorithm succeeds for families of distributions that satisfy two well-studied properties in prior works on robust estimation: certifiable subgaussianity of directional moments and certifiable hypercontractivity of degree 2 polynomials. Our recovery guarantees hold in the "right affine-invariant norms": Mahalanobis distance for mean, multiplicative spectral and relative Frobenius distance guarantees for covariance and injective norms for higher moments. Prior works obtained private robust algorithms for mean estimation of subgaussian distributions with bounded covariance. For covariance estimation, ours is the first efficient algorithm (even in the absence of outliers) that succeeds without any condition-number assumptions. Our algorithms arise from a new framework that provides a general blueprint for modifying convex relaxations for robust estimation to satisfy strong worst-case stability guarantees in the appropriate parameter norms whenever the algorithms produce witnesses of correctness in their run. We verify such guarantees for a modification of standard sum-of-squares (SoS) semidefinite programming relaxations for robust estimation. Our privacy guarantees are obtained by combining stability guarantees with a new "estimate dependent" noise injection mechanism in which noise scales with the eigenvalues of the estimated covariance. We believe this framework will be useful more generally in obtaining DP counterparts of robust estimators. Independently of our work, Ashtiani and Liaw [AL21] also obtained a polynomial time and sample private robust estimation algorithm for Gaussian distributions.

User-Level Private Learning via Correlated Sampling

Most works in learning with differential privacy (DP) have focused on the setting where each user has a single sample. In this work, we consider the setting where each user holds $m$ samples and the privacy protection is enforced at the level of each user's data. We show that, in this setting, we may learn with a much fewer number of users. Specifically, we show that, as long as each user receives sufficiently many samples, we can learn any privately learnable class via an $(\epsilon, \delta)$-DP algorithm using only $O(\log(1/\delta)/\epsilon)$ users. For $\epsilon$-DP algorithms, we show that we can learn using only $O_{\epsilon}(d)$ users even in the local model, where $d$ is the probabilistic representation dimension. In both cases, we show a nearly-matching lower bound on the number of users required. A crucial component of our results is a generalization of global stability [Bun et al., FOCS 2020] that allows the use of public randomness. Under this relaxed notion, we employ a correlated sampling strategy to show that the global stability can be boosted to be arbitrarily close to one, at a polynomial expense in the number of samples.

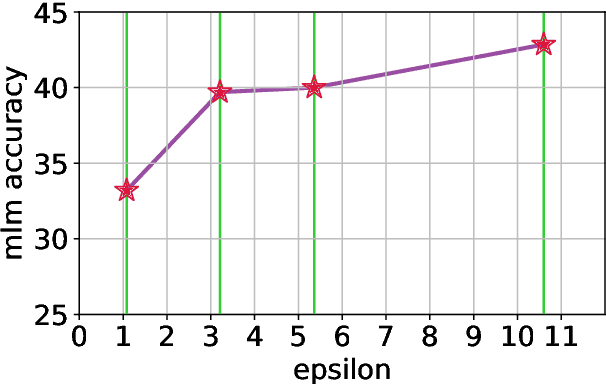
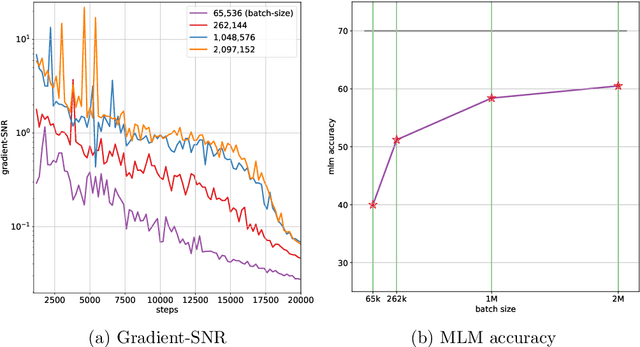
Large-Scale Differentially Private BERT

In this work, we study the large-scale pretraining of BERT-Large with differentially private SGD (DP-SGD). We show that combined with a careful implementation, scaling up the batch size to millions (i.e., mega-batches) improves the utility of the DP-SGD step for BERT; we also enhance its efficiency by using an increasing batch size schedule. Our implementation builds on the recent work of [SVK20], who demonstrated that the overhead of a DP-SGD step is minimized with effective use of JAX [BFH+18, FJL18] primitives in conjunction with the XLA compiler [XLA17]. Our implementation achieves a masked language model accuracy of 60.5% at a batch size of 2M, for $\epsilon = 5.36$. To put this number in perspective, non-private BERT models achieve an accuracy of $\sim$70%.

Contextual Recommendations and Low-Regret Cutting-Plane Algorithms

We consider the following variant of contextual linear bandits motivated by routing applications in navigational engines and recommendation systems. We wish to learn a hidden $d$-dimensional value $w^*$. Every round, we are presented with a subset $\mathcal{X}_t \subseteq \mathbb{R}^d$ of possible actions. If we choose (i.e. recommend to the user) action $x_t$, we obtain utility $\langle x_t, w^* \rangle$ but only learn the identity of the best action $\arg\max_{x \in \mathcal{X}_t} \langle x, w^* \rangle$. We design algorithms for this problem which achieve regret $O(d\log T)$ and $\exp(O(d \log d))$. To accomplish this, we design novel cutting-plane algorithms with low "regret" -- the total distance between the true point $w^*$ and the hyperplanes the separation oracle returns. We also consider the variant where we are allowed to provide a list of several recommendations. In this variant, we give an algorithm with $O(d^2 \log d)$ regret and list size $\mathrm{poly}(d)$. Finally, we construct nearly tight algorithms for a weaker variant of this problem where the learner only learns the identity of an action that is better than the recommendation. Our results rely on new algorithmic techniques in convex geometry (including a variant of Steiner's formula for the centroid of a convex set) which may be of independent interest.