Robust Shape Regularity Criteria for Superpixel Evaluation

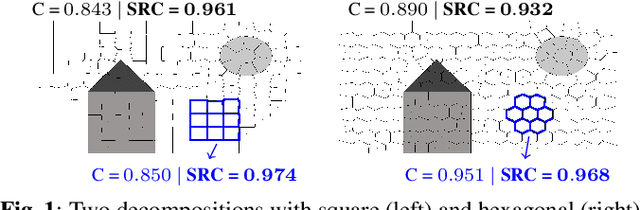
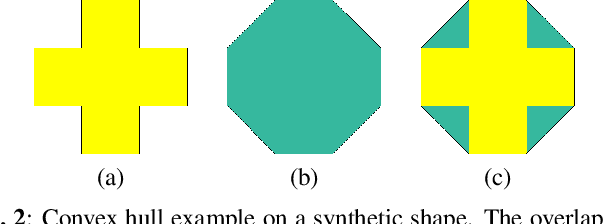
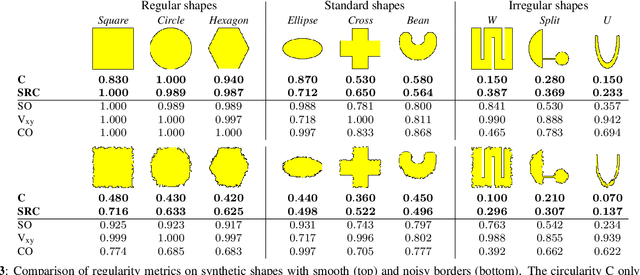
Regular decompositions are necessary for most superpixel-based object recognition or tracking applications. So far in the literature, the regularity or compactness of a superpixel shape is mainly measured by its circularity. In this work, we first demonstrate that such measure is not adapted for superpixel evaluation, since it does not directly express regularity but circular appearance. Then, we propose a new metric that considers several shape regularity aspects: convexity, balanced repartition, and contour smoothness. Finally, we demonstrate that our measure is robust to scale and noise and enables to more relevantly compare superpixel methods.

Superpixel-based Color Transfer

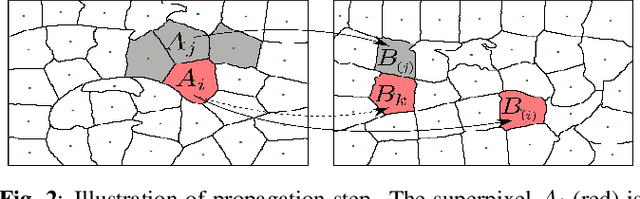
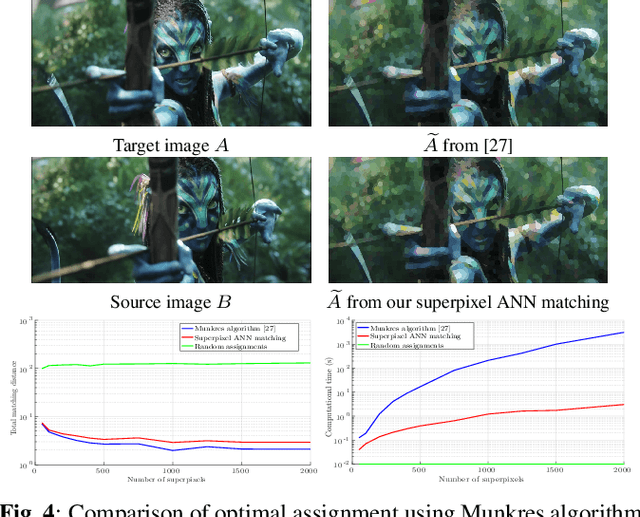
In this work, we propose a fast superpixel-based color transfer method (SCT) between two images. Superpixels enable to decrease the image dimension and to extract a reduced set of color candidates. We propose to use a fast approximate nearest neighbor matching algorithm in which we enforce the match diversity by limiting the selection of the same superpixels. A fusion framework is designed to transfer the matched colors, and we demonstrate the improvement obtained over exact matching results. Finally, we show that SCT is visually competitive compared to state-of-the-art methods.

Texture-Aware Superpixel Segmentation

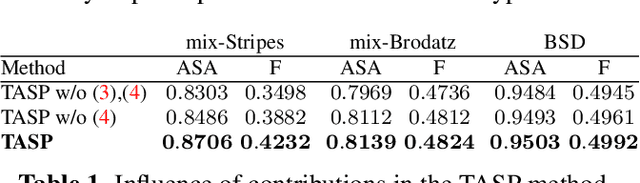
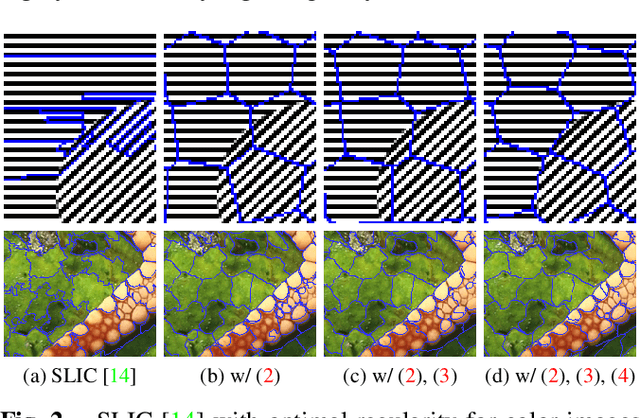
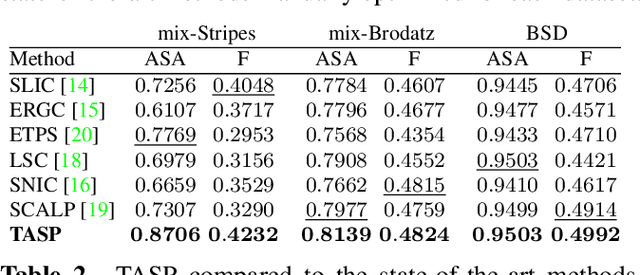
Most superpixel algorithms compute a trade-off between spatial and color features at the pixel level. Hence, they may need fine parameter tuning to balance the two measures, and highly fail to group pixels with similar local texture properties. In this paper, we address these issues with a new Texture-Aware SuperPixel (TASP) method. To accurately segment textured and smooth areas, TASP automatically adjusts its spatial constraint according to the local feature variance. Then, to ensure texture homogeneity within superpixels, a new pixel to superpixel patch-based distance is proposed. TASP outperforms the segmentation accuracy of the state-of-the-art methods on texture and also natural color image datasets.

Semi-supervised Learning with Graphs: Covariance Based Superpixels For Hyperspectral Image Classification

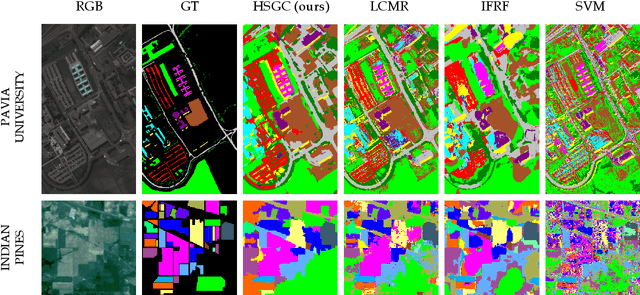
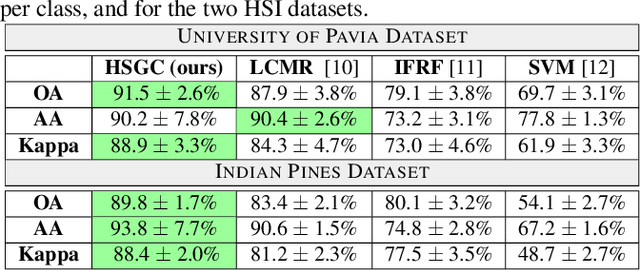
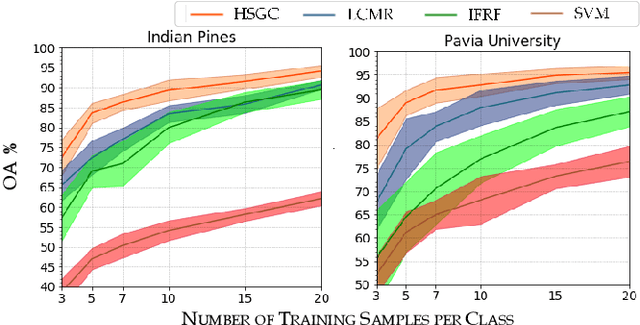
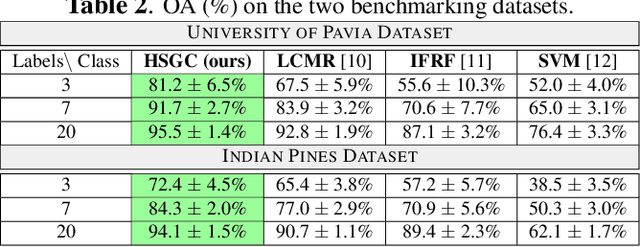
In this paper, we present a graph-based semi-supervised framework for hyperspectral image classification. We first introduce a novel superpixel algorithm based on the spectral covariance matrix representation of pixels to provide a better representation of our data. We then construct a superpixel graph, based on carefully considered feature vectors, before performing classification. We demonstrate, through a set of experimental results using two benchmarking datasets, that our approach outperforms three state-of-the-art classification frameworks, especially when an extremely small amount of labelled data is used.

Regularized Optimal Transport and the Rot Mover's Distance

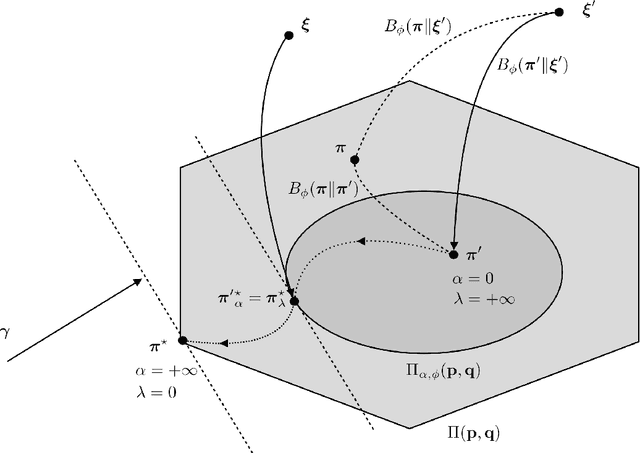
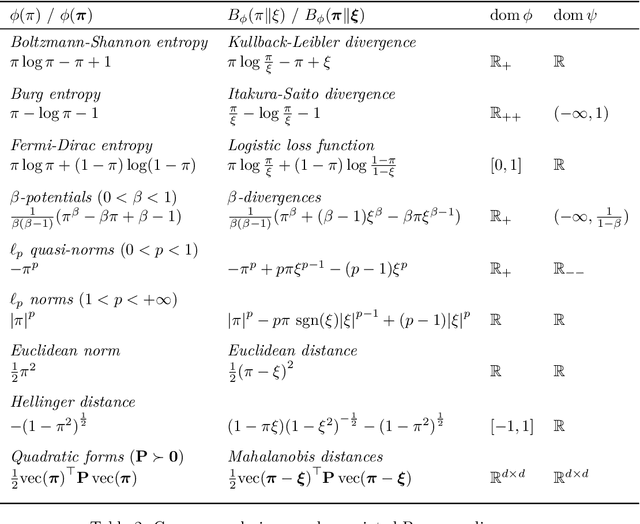
This paper presents a unified framework for smooth convex regularization of discrete optimal transport problems. In this context, the regularized optimal transport turns out to be equivalent to a matrix nearness problem with respect to Bregman divergences. Our framework thus naturally generalizes a previously proposed regularization based on the Boltzmann-Shannon entropy related to the Kullback-Leibler divergence, and solved with the Sinkhorn-Knopp algorithm. We call the regularized optimal transport distance the rot mover's distance in reference to the classical earth mover's distance. We develop two generic schemes that we respectively call the alternate scaling algorithm and the non-negative alternate scaling algorithm, to compute efficiently the regularized optimal plans depending on whether the domain of the regularizer lies within the non-negative orthant or not. These schemes are based on Dykstra's algorithm with alternate Bregman projections, and further exploit the Newton-Raphson method when applied to separable divergences. We enhance the separable case with a sparse extension to deal with high data dimensions. We also instantiate our proposed framework and discuss the inherent specificities for well-known regularizers and statistical divergences in the machine learning and information geometry communities. Finally, we demonstrate the merits of our methods with experiments using synthetic data to illustrate the effect of different regularizers and penalties on the solutions, as well as real-world data for a pattern recognition application to audio scene classification.

Parameter Estimation in Finite Mixture Models by Regularized Optimal Transport: A Unified Framework for Hard and Soft Clustering

In this short paper, we formulate parameter estimation for finite mixture models in the context of discrete optimal transportation with convex regularization. The proposed framework unifies hard and soft clustering methods for general mixture models. It also generalizes the celebrated $k$\nobreakdash-means and expectation-maximization algorithms in relation to associated Bregman divergences when applied to exponential family mixture models.

Characterizing the maximum parameter of the total-variation denoising through the pseudo-inverse of the divergence

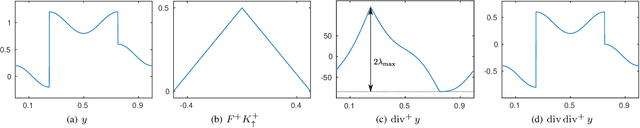
We focus on the maximum regularization parameter for anisotropic total-variation denoising. It corresponds to the minimum value of the regularization parameter above which the solution remains constant. While this value is well know for the Lasso, such a critical value has not been investigated in details for the total-variation. Though, it is of importance when tuning the regularization parameter as it allows fixing an upper-bound on the grid for which the optimal parameter is sought. We establish a closed form expression for the one-dimensional case, as well as an upper-bound for the two-dimensional case, that appears reasonably tight in practice. This problem is directly linked to the computation of the pseudo-inverse of the divergence, which can be quickly obtained by performing convolutions in the Fourier domain.

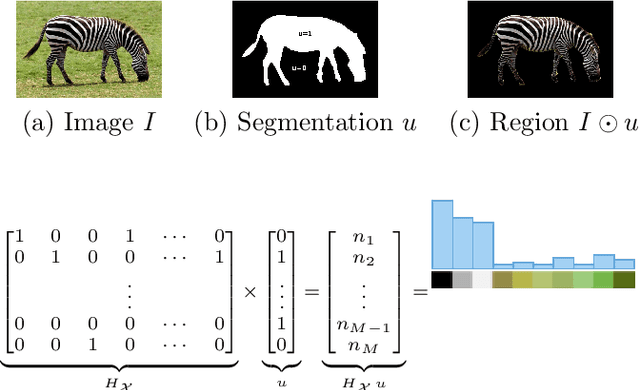
Convex Histogram-Based Joint Image Segmentation with Regularized Optimal Transport Cost

We investigate in this work a versatile convex framework for multiple image segmentation, relying on the regularized optimal mass transport theory. In this setting, several transport cost functions are considered and used to match statistical distributions of features. In practice, global multidimensional histograms are estimated from the segmented image regions, and are compared to referring models that are either fixed histograms given a priori, or directly inferred in the non-supervised case. The different convex problems studied are solved efficiently using primal-dual algorithms. The proposed approach is generic and enables multi-phase segmentation as well as co-segmentation of multiple images.

Convex Color Image Segmentation with Optimal Transport Distances

This work is about the use of regularized optimal-transport distances for convex, histogram-based image segmentation. In the considered framework, fixed exemplar histograms define a prior on the statistical features of the two regions in competition. In this paper, we investigate the use of various transport-based cost functions as discrepancy measures and rely on a primal-dual algorithm to solve the obtained convex optimization problem.

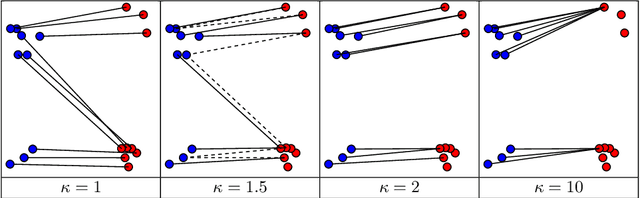
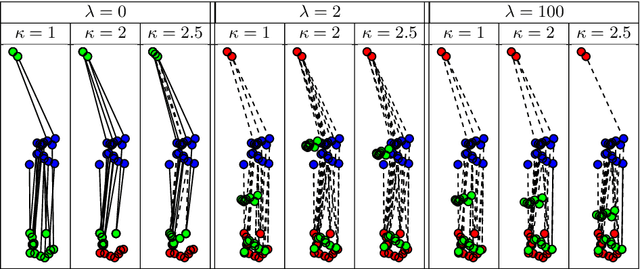
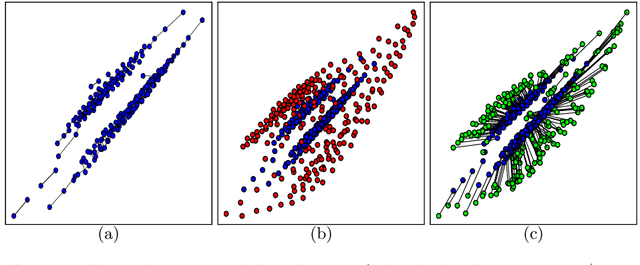
Regularized Discrete Optimal Transport

This article introduces a generalization of the discrete optimal transport, with applications to color image manipulations. This new formulation includes a relaxation of the mass conservation constraint and a regularization term. These two features are crucial for image processing tasks, which necessitate to take into account families of multimodal histograms, with large mass variation across modes. The corresponding relaxed and regularized transportation problem is the solution of a convex optimization problem. Depending on the regularization used, this minimization can be solved using standard linear programming methods or first order proximal splitting schemes. The resulting transportation plan can be used as a color transfer map, which is robust to mass variation across images color palettes. Furthermore, the regularization of the transport plan helps to remove colorization artifacts due to noise amplification. We also extend this framework to the computation of barycenters of distributions. The barycenter is the solution of an optimization problem, which is separately convex with respect to the barycenter and the transportation plans, but not jointly convex. A block coordinate descent scheme converges to a stationary point of the energy. We show that the resulting algorithm can be used for color normalization across several images. The relaxed and regularized barycenter defines a common color palette for those images. Applying color transfer toward this average palette performs a color normalization of the input images.