Photo-unrealistic Image Enhancement for Subject Placement in Outdoor Photography

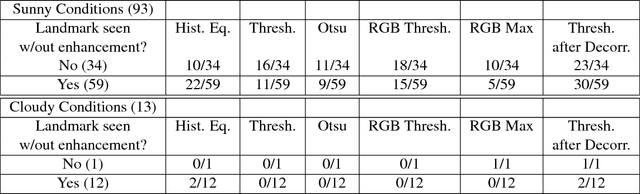
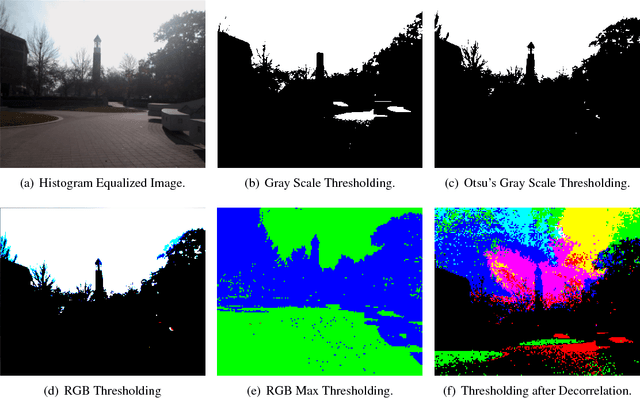
Camera display reflections are an issue in bright light situations, as they may prevent users from correctly positioning the subject in the picture. We propose a software solution to this problem, which consists in modifying the image in the viewer, in real time. In our solution, the user is seeing a posterized image which roughly represents the contour of the objects. Five enhancement methods are compared in a user study. Our results indicate that the problem considered is a valid one, as users had problems locating landmarks nearly 37% of the time under sunny conditions, and that our proposed enhancement method using contrasting colors is a practical solution to that problem.

Pattern Dependence Detection using n-TARP Clustering

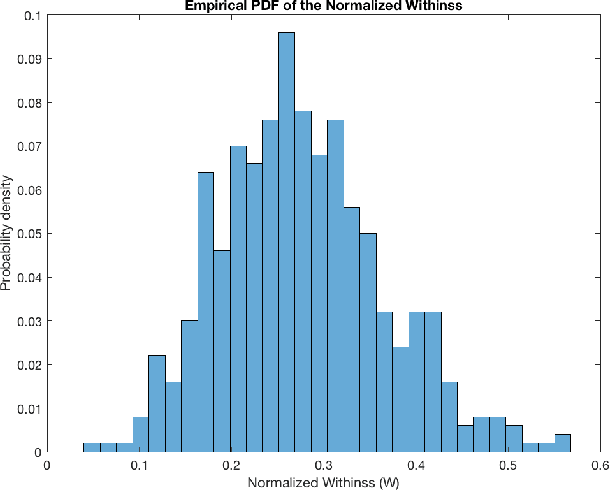
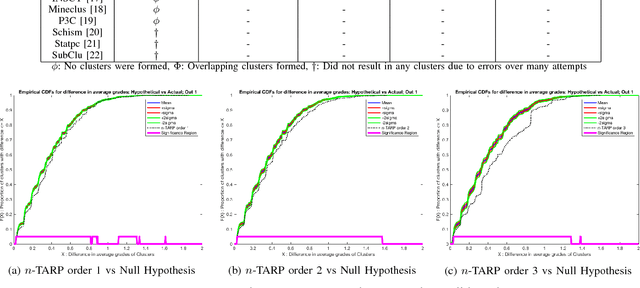
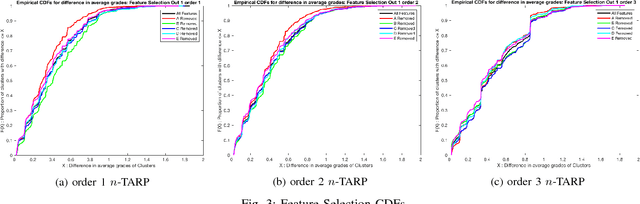
Consider an experiment involving a potentially small number of subjects. Some random variables are observed on each subject: a high-dimensional one called the "observed" random variable, and a one-dimensional one called the "outcome" random variable. We are interested in the dependencies between the observed random variable and the outcome random variable. We propose a method to quantify and validate the dependencies of the outcome random variable on the various patterns contained in the observed random variable. Different degrees of relationship are explored (linear, quadratic, cubic, ...). This work is motivated by the need to analyze educational data, which often involves high-dimensional data representing a small number of students. Thus our implementation is designed for a small number of subjects; however, it can be easily modified to handle a very large dataset. As an illustration, the proposed method is used to study the influence of certain skills on the course grade of students in a signal processing class. A valid dependency of the grade on the different skill patterns is observed in the data.

Benchmarks for Image Classification and Other High-dimensional Pattern Recognition Problems

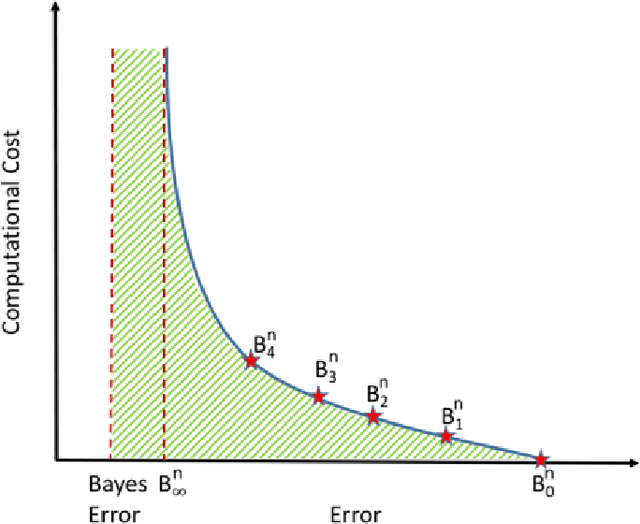
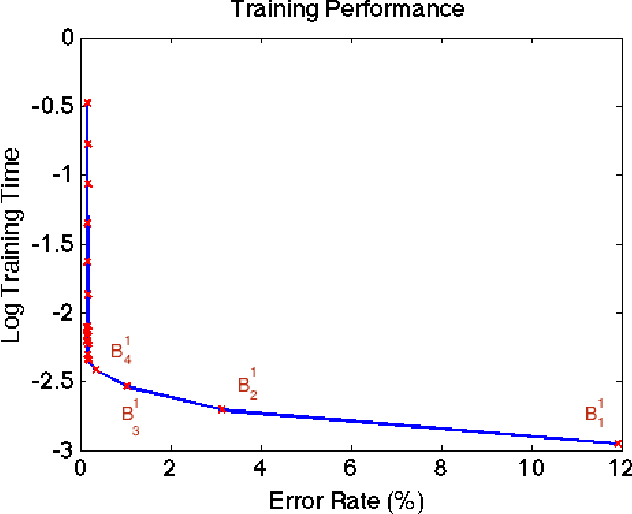
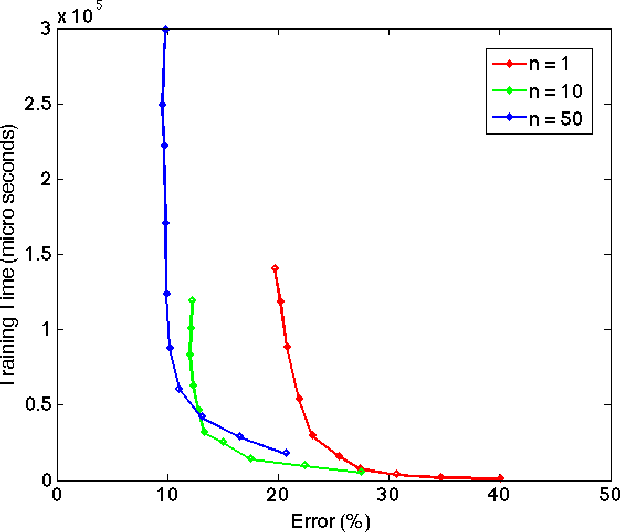
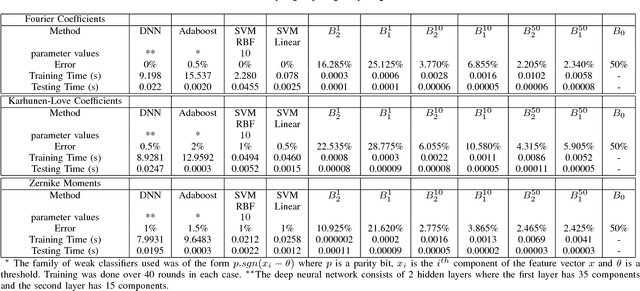
A good classification method should yield more accurate results than simple heuristics. But there are classification problems, especially high-dimensional ones like the ones based on image/video data, for which simple heuristics can work quite accurately; the structure of the data in such problems is easy to uncover without any sophisticated or computationally expensive method. On the other hand, some problems have a structure that can only be found with sophisticated pattern recognition methods. We are interested in quantifying the difficulty of a given high-dimensional pattern recognition problem. We consider the case where the patterns come from two pre-determined classes and where the objects are represented by points in a high-dimensional vector space. However, the framework we propose is extendable to an arbitrarily large number of classes. We propose classification benchmarks based on simple random projection heuristics. Our benchmarks are 2D curves parameterized by the classification error and computational cost of these simple heuristics. Each curve divides the plane into a "positive- gain" and a "negative-gain" region. The latter contains methods that are ill-suited for the given classification problem. The former is divided into two by the curve asymptote; methods that lie in the small region under the curve but right of the asymptote merely provide a computational gain but no structural advantage over the random heuristics. We prove that the curve asymptotes are optimal (i.e. at Bayes error) in some cases, and thus no sophisticated method can provide a structural advantage over the random heuristics. Such classification problems, an example of which we present in our numerical experiments, provide poor ground for testing new pattern classification methods.

The Pascal Triangle of a Discrete Image: Definition, Properties and Application to Shape Analysis

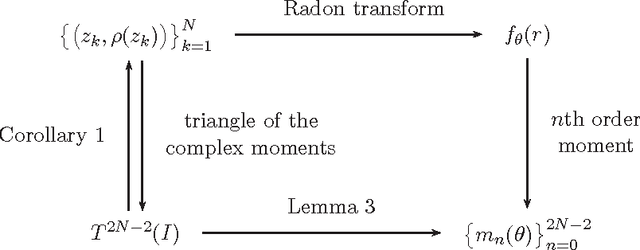
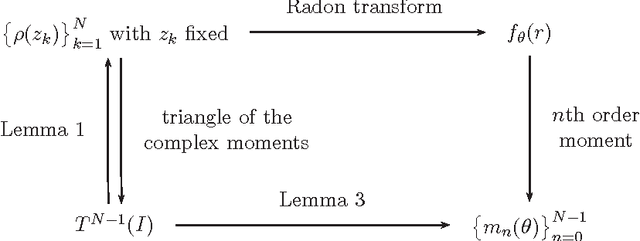
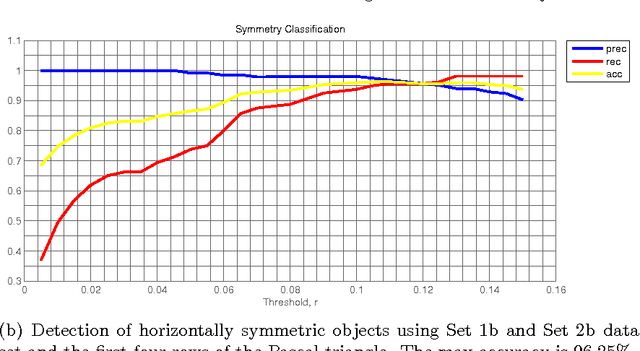
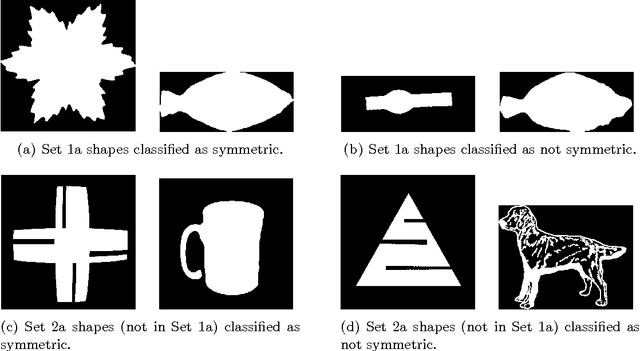
We define the Pascal triangle of a discrete (gray scale) image as a pyramidal arrangement of complex-valued moments and we explore its geometric significance. In particular, we show that the entries of row k of this triangle correspond to the Fourier series coefficients of the moment of order k of the Radon transform of the image. Group actions on the plane can be naturally prolonged onto the entries of the Pascal triangle. We study the prolongation of some common group actions, such as rotations and reflections, and we propose simple tests for detecting equivalences and self-equivalences under these group actions. The motivating application of this work is the problem of characterizing the geometry of objects on images, for example by detecting approximate symmetries.

Automatic Text Area Segmentation in Natural Images

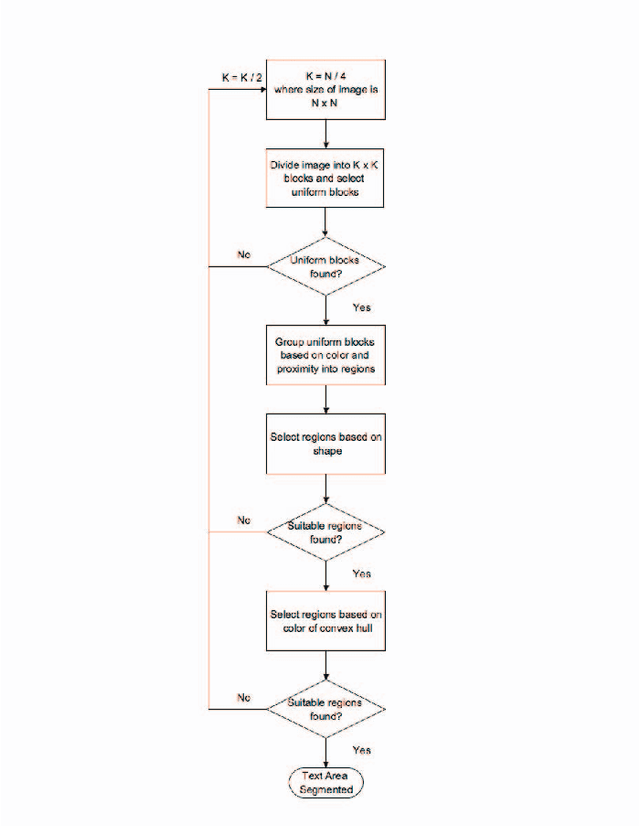
We present a hierarchical method for segmenting text areas in natural images. The method assumes that the text is written with a contrasting color on a more or less uniform background. But no assumption is made regarding the language or character set used to write the text. In particular, the text can contain simple graphics or symbols. The key feature of our approach is that we first concentrate on finding the background of the text, before testing whether there is actually text on the background. Since uniform areas are easy to find in natural images, and since text backgrounds define areas which contain "holes" (where the text is written) we thus look for uniform areas containing "holes" and label them as text backgrounds candidates. Each candidate area is then further tested for the presence of text within its convex hull. We tested our method on a database of 65 images including English and Urdu text. The method correctly segmented all the text areas in 63 of these images, and in only 4 of these were areas that do not contain text also segmented.

Lossless Representation of Graphs using Distributions

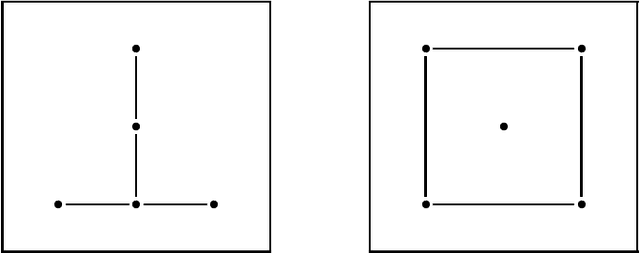
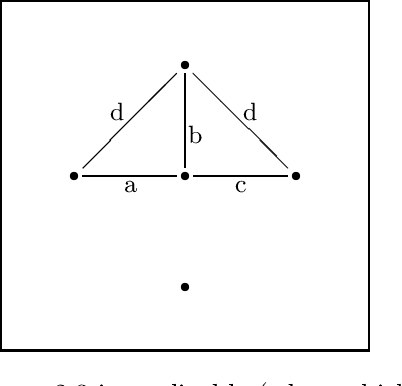
We consider complete graphs with edge weights and/or node weights taking values in some set. In the first part of this paper, we show that a large number of graphs are completely determined, up to isomorphism, by the distribution of their sub-triangles. In the second part, we propose graph representations in terms of one-dimensional distributions (e.g., distribution of the node weights, sum of adjacent weights, etc.). For the case when the weights of the graph are real-valued vectors, we show that all graphs, except for a set of measure zero, are uniquely determined, up to isomorphism, from these distributions. The motivating application for this paper is the problem of browsing through large sets of graphs.

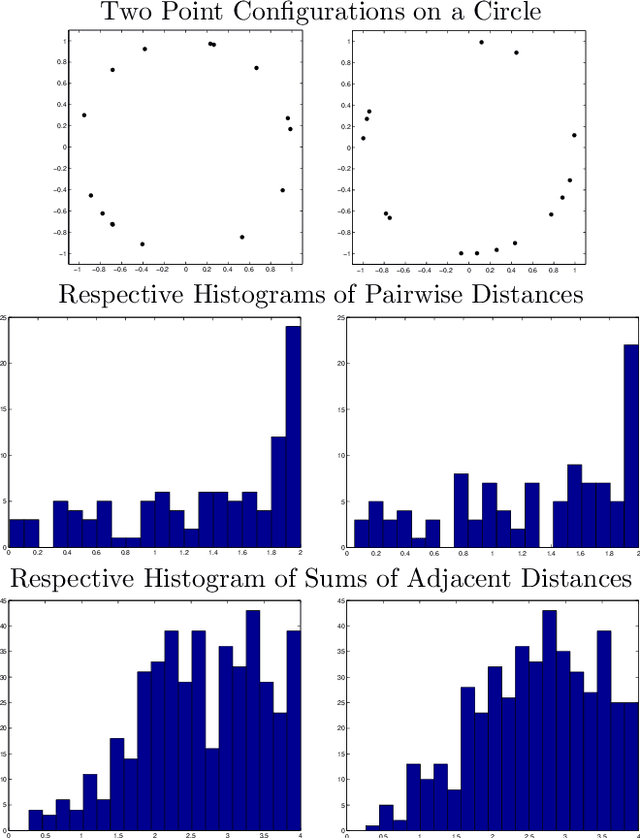
Which Point Configurations are Determined by the Distribution of their Pairwise Distances?

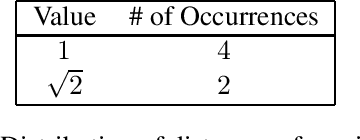
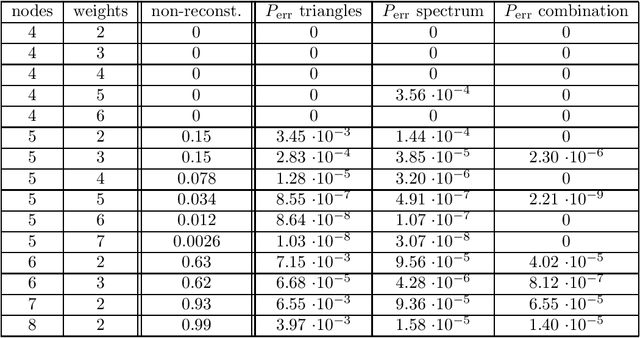
In a previous paper we showed that, for any $n \ge m+2$, most sets of $n$ points in $\RR^m$ are determined (up to rotations, reflections, translations and relabeling of the points) by the distribution of their pairwise distances. But there are some exceptional point configurations which are not reconstructible from the distribution of distances in the above sense. In this paper, we present a reconstructibility test with running time $O(n^{11})$. The cases of orientation preserving rigid motions (rotations and translations) and scalings are also discussed.

On reconstructing n-point configurations from the distribution of distances or areas

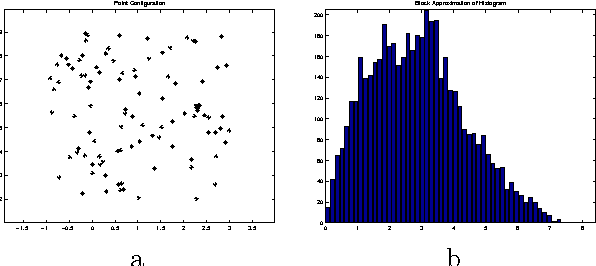
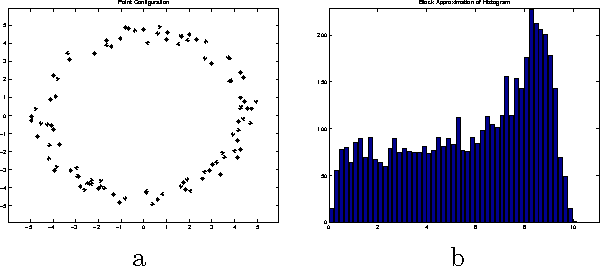
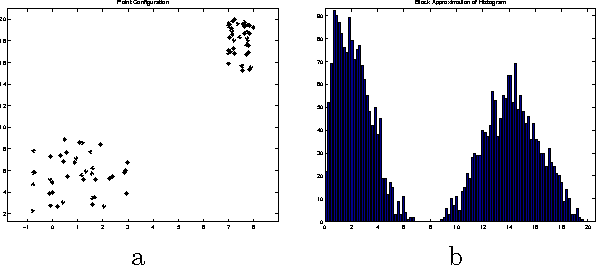
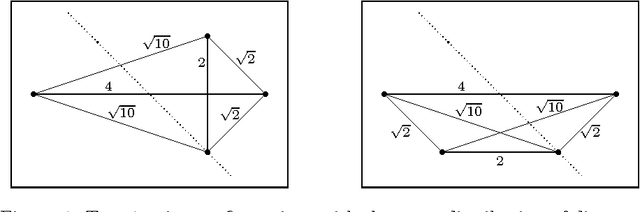
One way to characterize configurations of points up to congruence is by considering the distribution of all mutual distances between points. This paper deals with the question if point configurations are uniquely determined by this distribution. After giving some counterexamples, we prove that this is the case for the vast majority of configurations. In the second part of the paper, the distribution of areas of sub-triangles is used for characterizing point configurations. Again it turns out that most configurations are reconstructible from the distribution of areas, though there are counterexamples.

Structure from Motion: Theoretical Foundations of a Novel Approach Using Custom Built Invariants

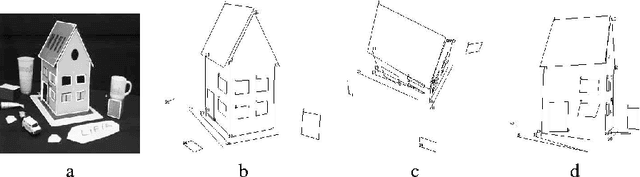
We rephrase the problem of 3D reconstruction from images in terms of intersections of projections of orbits of custom built Lie groups actions. We then use an algorithmic method based on moving frames "a la Fels-Olver" to obtain a fundamental set of invariants of these groups actions. The invariants are used to define a set of equations to be solved by the points of the 3D object, providing a new technique for recovering 3D structure from motion.

Numerically Invariant Signature Curves

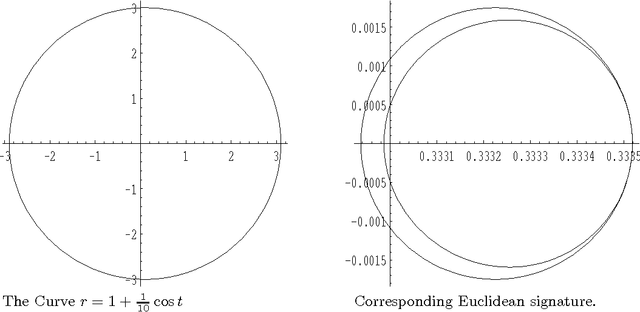
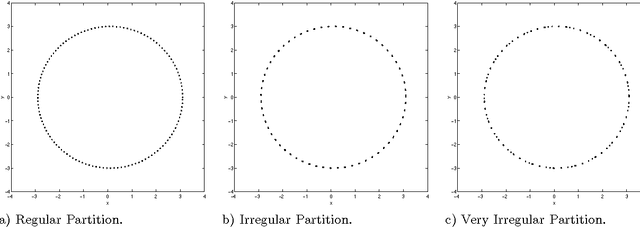
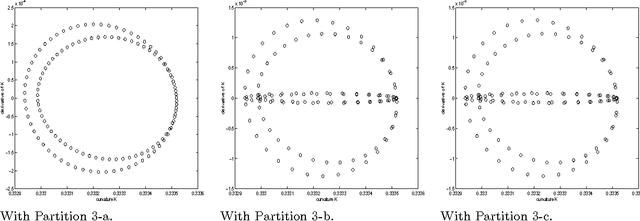
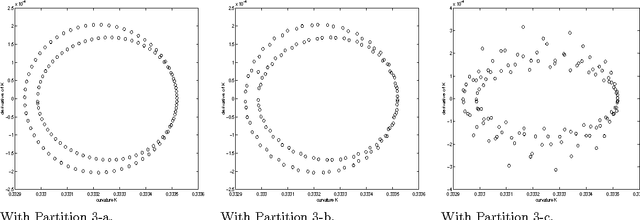
Corrected versions of the numerically invariant expressions for the affine and Euclidean signature of a planar curve proposed by E.Calabi et. al are presented. The new formulas are valid for fine but otherwise arbitrary partitions of the curve. We also give numerically invariant expressions for the four differential invariants parametrizing the three dimensional version of the Euclidean signature curve, namely the curvature, the torsion and their derivatives with respect to arc length.