SETA: Statistical Fault Attribution for Compound AI Systems

Modern AI systems increasingly comprise multiple interconnected neural networks to tackle complex inference tasks. Testing such systems for robustness and safety entails significant challenges. Current state-of-the-art robustness testing techniques, whether black-box or white-box, have been proposed and implemented for single-network models and do not scale well to multi-network pipelines. We propose a modular robustness testing framework that applies a given set of perturbations to test data. Our testing framework supports (1) a component-wise system analysis to isolate errors and (2) reasoning about error propagation across the neural network modules. The testing framework is architecture and modality agnostic and can be applied across domains. We apply the framework to a real-world autonomous rail inspection system composed of multiple deep networks and successfully demonstrate how our approach enables fine-grained robustness analysis beyond conventional end-to-end metrics.

LipBaB: Computing exact Lipschitz constant of ReLU networks

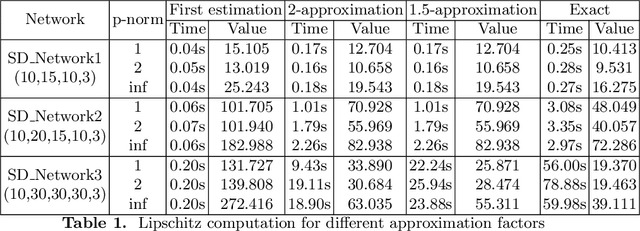
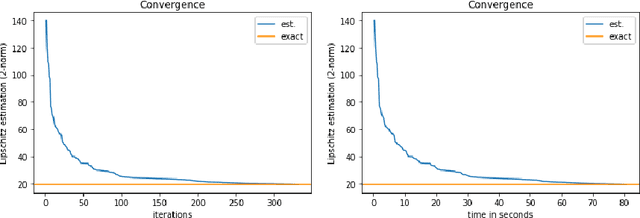
The Lipschitz constant of neural networks plays an important role in several contexts of deep learning ranging from robustness certification and regularization to stability analysis of systems with neural network controllers. Obtaining tight bounds of the Lipschitz constant is therefore important. We introduce LipBaB, a branch and bound framework to compute certified bounds of the local Lipschitz constant of deep neural networks with ReLU activation functions up to any desired precision. We achieve this by bounding the norm of the Jacobians, corresponding to different activation patterns of the network caused within the input domain. Our algorithm can provide provably exact computation of the Lipschitz constant for any p-norm.