Transformers learn factored representations

Transformers pretrained via next token prediction learn to factor their world into parts, representing these factors in orthogonal subspaces of the residual stream. We formalize two representational hypotheses: (1) a representation in the product space of all factors, whose dimension grows exponentially with the number of parts, or (2) a factored representation in orthogonal subspaces, whose dimension grows linearly. The factored representation is lossless when factors are conditionally independent, but sacrifices predictive fidelity otherwise, creating a tradeoff between dimensional efficiency and accuracy. We derive precise predictions about the geometric structure of activations for each, including the number of subspaces, their dimensionality, and the arrangement of context embeddings within them. We test between these hypotheses on transformers trained on synthetic processes with known latent structure. Models learn factored representations when factors are conditionally independent, and continue to favor them early in training even when noise or hidden dependencies undermine conditional independence, reflecting an inductive bias toward factoring at the cost of fidelity. This provides a principled explanation for why transformers decompose the world into parts, and suggests that interpretable low dimensional structure may persist even in models trained on complex data.

All-Action Policy Gradient Methods: A Numerical Integration Approach

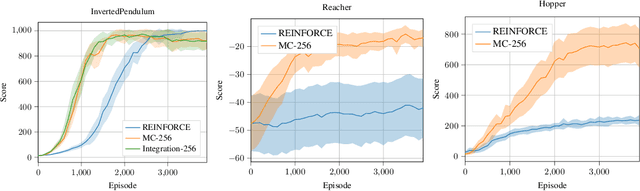
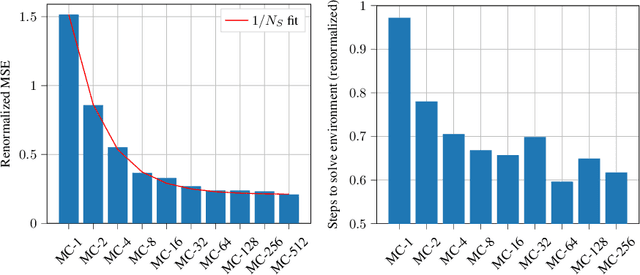
While often stated as an instance of the likelihood ratio trick [Rubinstein, 1989], the original policy gradient theorem [Sutton, 1999] involves an integral over the action space. When this integral can be computed, the resulting "all-action" estimator [Sutton, 2001] provides a conditioning effect [Bratley, 1987] reducing the variance significantly compared to the REINFORCE estimator [Williams, 1992]. In this paper, we adopt a numerical integration perspective to broaden the applicability of the all-action estimator to general spaces and to any function class for the policy or critic components, beyond the Gaussian case considered by [Ciosek, 2018]. In addition, we provide a new theoretical result on the effect of using a biased critic which offers more guidance than the previous "compatible features" condition of [Sutton, 1999]. We demonstrate the benefit of our approach in continuous control tasks with nonlinear function approximation. Our results show improved performance and sample efficiency.