Adaptive and Calibrated Ensemble Learning with Dependent Tail-free Process

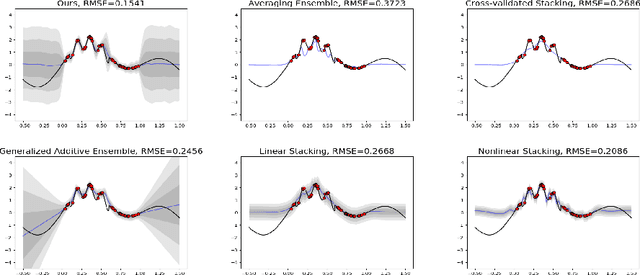
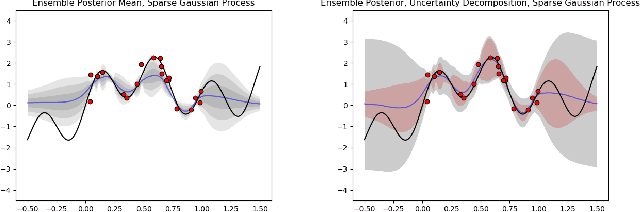
Ensemble learning is a mainstay in modern data science practice. Conventional ensemble algorithms assigns to base models a set of deterministic, constant model weights that (1) do not fully account for variations in base model accuracy across subgroups, nor (2) provide uncertainty estimates for the ensemble prediction, which could result in mis-calibrated (i.e. precise but biased) predictions that could in turn negatively impact the algorithm performance in real-word applications. In this work, we present an adaptive, probabilistic approach to ensemble learning using dependent tail-free process as ensemble weight prior. Given input feature $\mathbf{x}$, our method optimally combines base models based on their predictive accuracy in the feature space $\mathbf{x} \in \mathcal{X}$, and provides interpretable uncertainty estimates both in model selection and in ensemble prediction. To encourage scalable and calibrated inference, we derive a structured variational inference algorithm that jointly minimize KL objective and the model's calibration score (i.e. Continuous Ranked Probability Score (CRPS)). We illustrate the utility of our method on both a synthetic nonlinear function regression task, and on the real-world application of spatio-temporal integration of particle pollution prediction models in New England.

Robust Hypothesis Test for Nonlinear Effect with Gaussian Processes

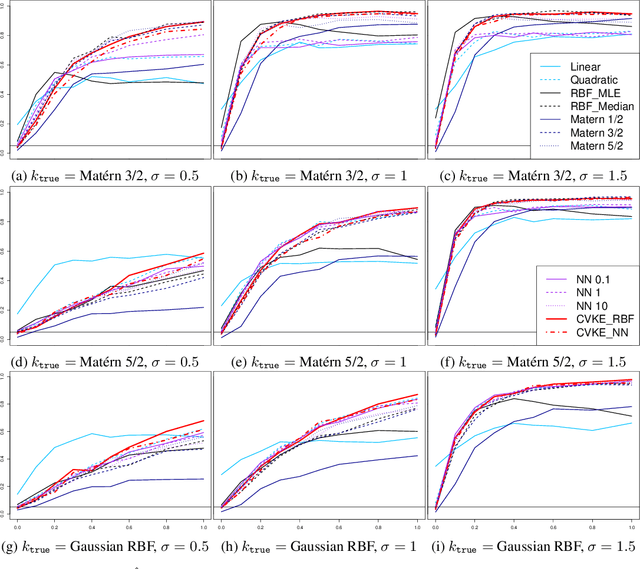
This work constructs a hypothesis test for detecting whether an data-generating function $h: R^p \rightarrow R$ belongs to a specific reproducing kernel Hilbert space $\mathcal{H}_0$ , where the structure of $\mathcal{H}_0$ is only partially known. Utilizing the theory of reproducing kernels, we reduce this hypothesis to a simple one-sided score test for a scalar parameter, develop a testing procedure that is robust against the mis-specification of kernel functions, and also propose an ensemble-based estimator for the null model to guarantee test performance in small samples. To demonstrate the utility of the proposed method, we apply our test to the problem of detecting nonlinear interaction between groups of continuous features. We evaluate the finite-sample performance of our test under different data-generating functions and estimation strategies for the null model. Our results reveal interesting connections between notions in machine learning (model underfit/overfit) and those in statistical inference (i.e. Type I error/power of hypothesis test), and also highlight unexpected consequences of common model estimating strategies (e.g. estimating kernel hyperparameters using maximum likelihood estimation) on model inference.