Set-valued dynamic treatment regimes for competing outcomes

Dynamic treatment regimes operationalize the clinical decision process as a sequence of functions, one for each clinical decision, where each function takes as input up-to-date patient information and gives as output a single recommended treatment. Current methods for estimating optimal dynamic treatment regimes, for example Q-learning, require the specification of a single outcome by which the `goodness' of competing dynamic treatment regimes are measured. However, this is an over-simplification of the goal of clinical decision making, which aims to balance several potentially competing outcomes. For example, often a balance must be struck between treatment effectiveness and side-effect burden. We propose a method for constructing dynamic treatment regimes that accommodates competing outcomes by recommending sets of treatments at each decision point. Formally, we construct a sequence of set-valued functions that take as input up-to-date patient information and give as output a recommended subset of the possible treatments. For a given patient history, the recommended set of treatments contains all treatments that are not inferior according to any of the competing outcomes. When there is more than one decision point, constructing these set-valued functions requires solving a non-trivial enumeration problem. We offer an exact enumeration algorithm by recasting the problem as a linear mixed integer program. The proposed methods are illustrated using data from a depression study and the CATIE schizophrenia study.

Small Sample Inference for Generalization Error in Classification Using the CUD Bound

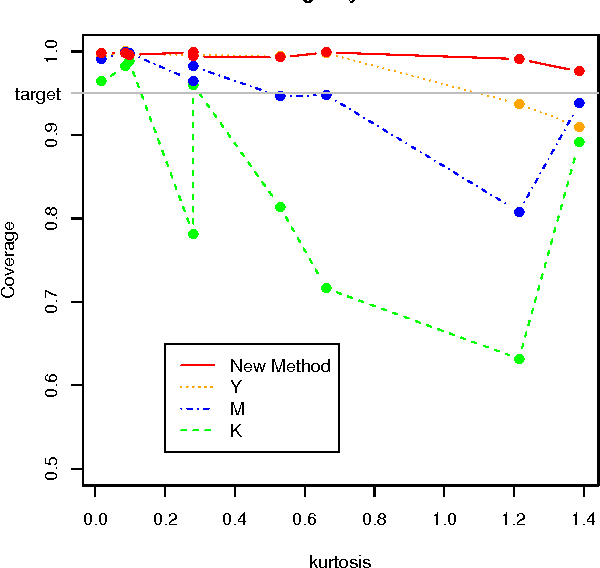
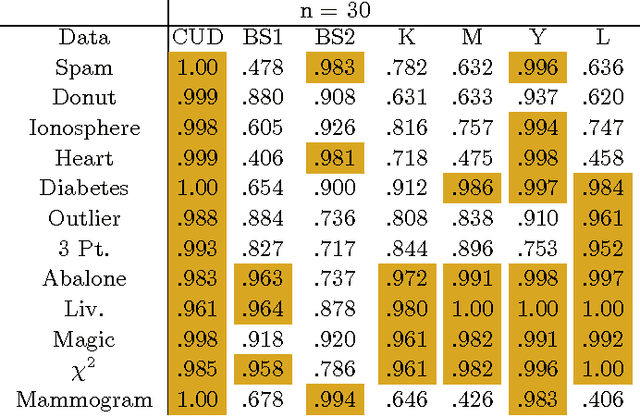
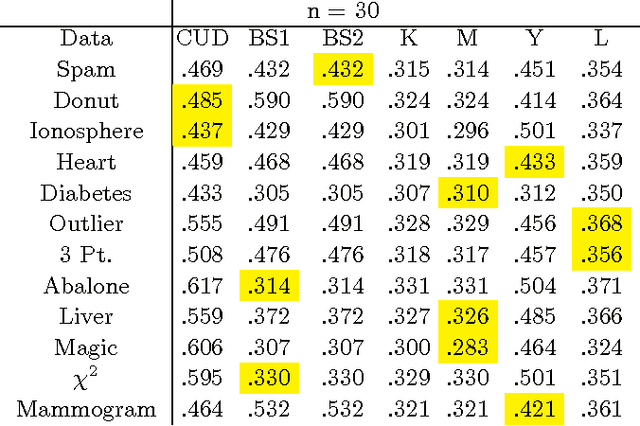
Confidence measures for the generalization error are crucial when small training samples are used to construct classifiers. A common approach is to estimate the generalization error by resampling and then assume the resampled estimator follows a known distribution to form a confidence set [Kohavi 1995, Martin 1996,Yang 2006]. Alternatively, one might bootstrap the resampled estimator of the generalization error to form a confidence set. Unfortunately, these methods do not reliably provide sets of the desired confidence. The poor performance appears to be due to the lack of smoothness of the generalization error as a function of the learned classifier. This results in a non-normal distribution of the estimated generalization error. We construct a confidence set for the generalization error by use of a smooth upper bound on the deviation between the resampled estimate and generalization error. The confidence set is formed by bootstrapping this upper bound. In cases in which the approximation class for the classifier can be represented as a parametric additive model, we provide a computationally efficient algorithm. This method exhibits superior performance across a series of test and simulated data sets.