Tighter Bounds on the Log Marginal Likelihood of Gaussian Process Regression Using Conjugate Gradients

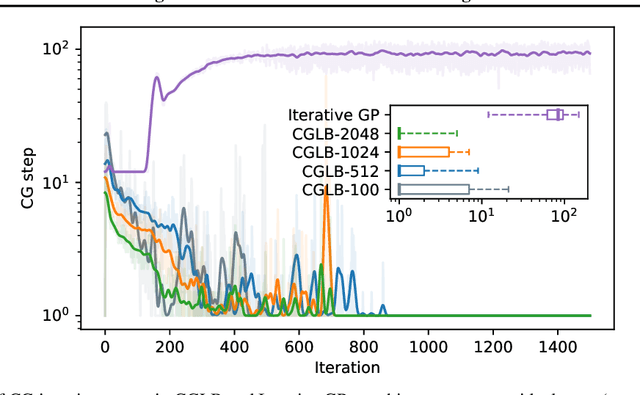
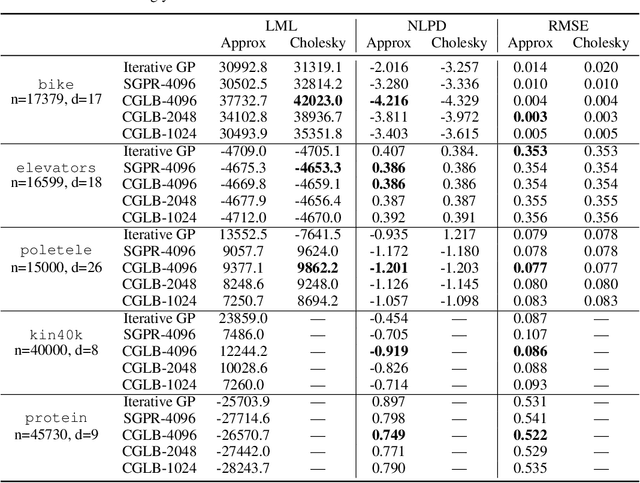
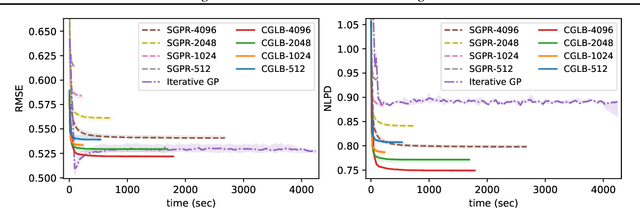
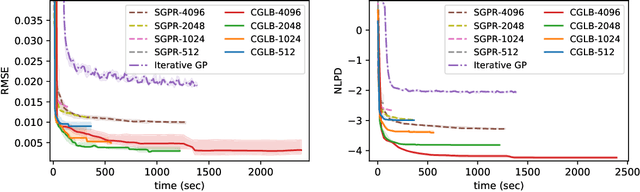
We propose a lower bound on the log marginal likelihood of Gaussian process regression models that can be computed without matrix factorisation of the full kernel matrix. We show that approximate maximum likelihood learning of model parameters by maximising our lower bound retains many of the sparse variational approach benefits while reducing the bias introduced into parameter learning. The basis of our bound is a more careful analysis of the log-determinant term appearing in the log marginal likelihood, as well as using the method of conjugate gradients to derive tight lower bounds on the term involving a quadratic form. Our approach is a step forward in unifying methods relying on lower bound maximisation (e.g. variational methods) and iterative approaches based on conjugate gradients for training Gaussian processes. In experiments, we show improved predictive performance with our model for a comparable amount of training time compared to other conjugate gradient based approaches.

Understanding Variational Inference in Function-Space

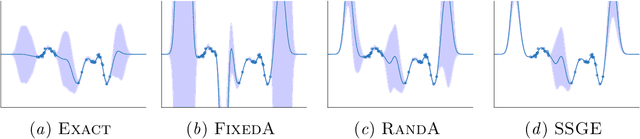
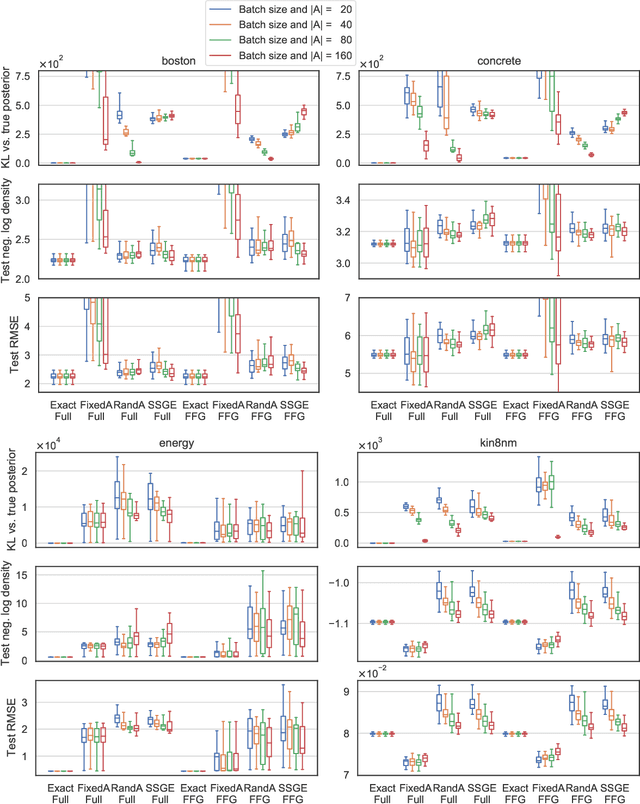
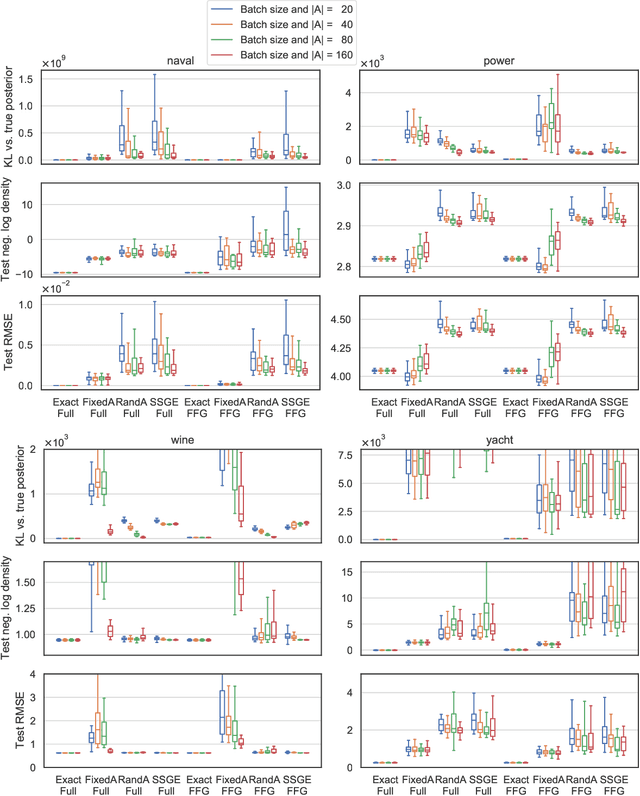
Recent work has attempted to directly approximate the `function-space' or predictive posterior distribution of Bayesian models, without approximating the posterior distribution over the parameters. This is appealing in e.g. Bayesian neural networks, where we only need the former, and the latter is hard to represent. In this work, we highlight some advantages and limitations of employing the Kullback-Leibler divergence in this setting. For example, we show that minimizing the KL divergence between a wide class of parametric distributions and the posterior induced by a (non-degenerate) Gaussian process prior leads to an ill-defined objective function. Then, we propose (featurized) Bayesian linear regression as a benchmark for `function-space' inference methods that directly measures approximation quality. We apply this methodology to assess aspects of the objective function and inference scheme considered in Sun, Zhang, Shi, and Grosse (2018), emphasizing the quality of approximation to Bayesian inference as opposed to predictive performance.

Convergence of Sparse Variational Inference in Gaussian Processes Regression

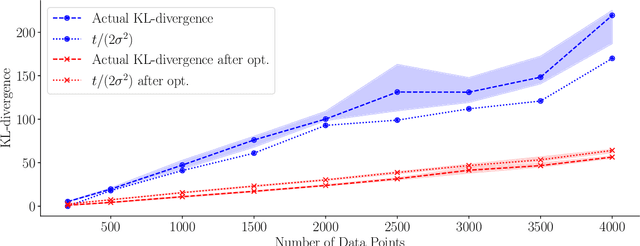
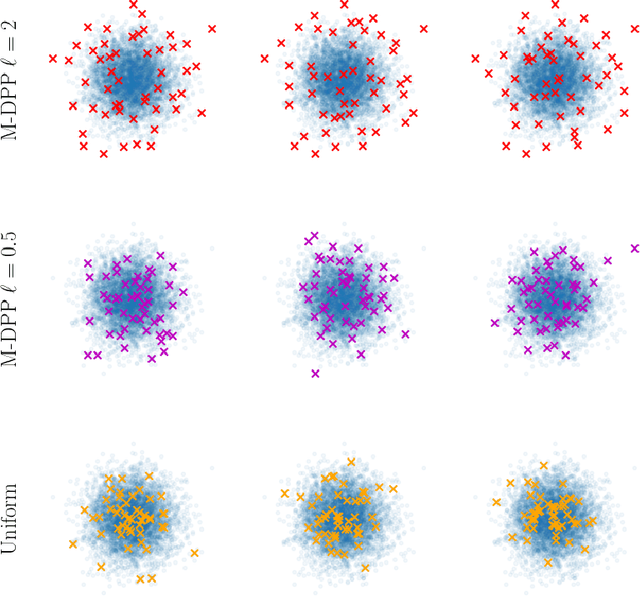
Gaussian processes are distributions over functions that are versatile and mathematically convenient priors in Bayesian modelling. However, their use is often impeded for data with large numbers of observations, $N$, due to the cubic (in $N$) cost of matrix operations used in exact inference. Many solutions have been proposed that rely on $M \ll N$ inducing variables to form an approximation at a cost of $\mathcal{O}(NM^2)$. While the computational cost appears linear in $N$, the true complexity depends on how $M$ must scale with $N$ to ensure a certain quality of the approximation. In this work, we investigate upper and lower bounds on how $M$ needs to grow with $N$ to ensure high quality approximations. We show that we can make the KL-divergence between the approximate model and the exact posterior arbitrarily small for a Gaussian-noise regression model with $M\ll N$. Specifically, for the popular squared exponential kernel and $D$-dimensional Gaussian distributed covariates, $M=\mathcal{O}((\log N)^D)$ suffice and a method with an overall computational cost of $\mathcal{O}(N(\log N)^{2D}(\log\log N)^2)$ can be used to perform inference.

Variational Orthogonal Features

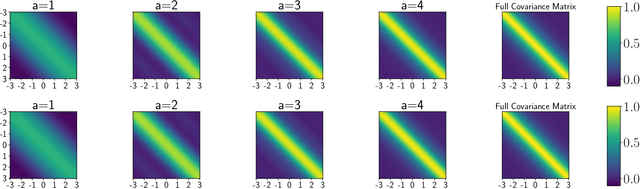
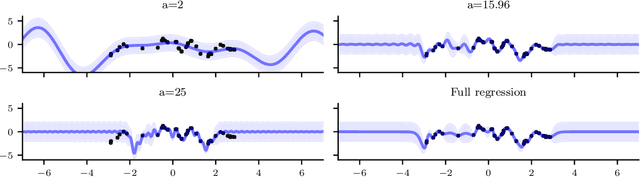
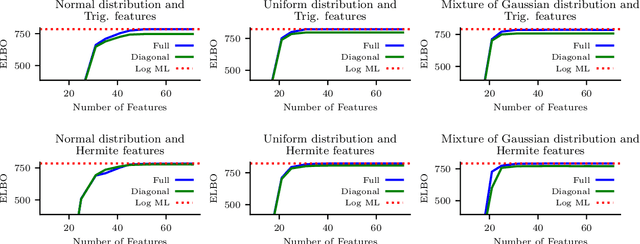
Sparse stochastic variational inference allows Gaussian process models to be applied to large datasets. The per iteration computational cost of inference with this method is $\mathcal{O}(\tilde{N}M^2+M^3),$ where $\tilde{N}$ is the number of points in a minibatch and $M$ is the number of `inducing features', which determine the expressiveness of the variational family. Several recent works have shown that for certain priors, features can be defined that remove the $\mathcal{O}(M^3)$ cost of computing a minibatch estimate of an evidence lower bound (ELBO). This represents a significant computational savings when $M\gg \tilde{N}$. We present a construction of features for any stationary prior kernel that allow for computation of an unbiased estimator to the ELBO using $T$ Monte Carlo samples in $\mathcal{O}(\tilde{N}T+M^2T)$ and in $\mathcal{O}(\tilde{N}T+MT)$ with an additional approximation. We analyze the impact of this additional approximation on inference quality.

Bandit optimisation of functions in the Matérn kernel RKHS

We consider the problem of optimising functions in the reproducing kernel Hilbert space (RKHS) of a Mat\'ern kernel with smoothness parameter $\nu$ over the domain $[0,1]^d$ under noisy bandit feedback. Our contribution, the $\pi$-GP-UCB algorithm, is the first practical approach with guaranteed sublinear regret for all $\nu>1$ and $d \geq 1$. Empirical validation suggests better performance and drastically improved computational scalablity compared with its predecessor, Improved GP-UCB.

Pathologies of Factorised Gaussian and MC Dropout Posteriors in Bayesian Neural Networks

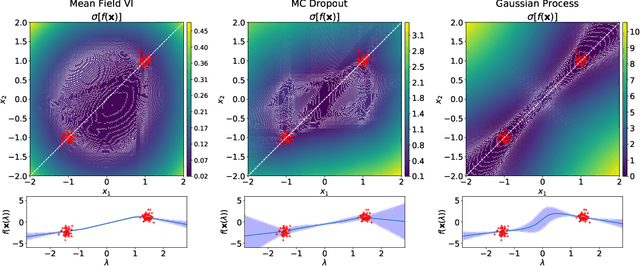
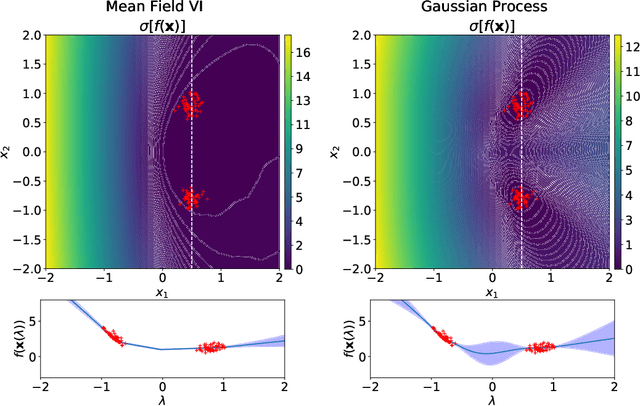
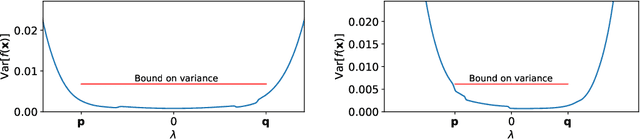
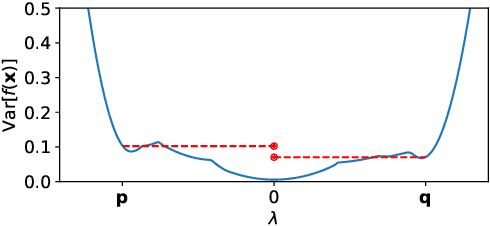
Neural networks provide state-of-the-art performance on a variety of tasks. However, they are often overconfident when making predictions. This inability to properly account for uncertainty limits their application to high-risk decision making, active learning and Bayesian optimisation. To address this, Bayesian inference has been proposed as a framework for improving uncertainty estimates. In practice, Bayesian neural networks rely on poorly understood approximations for computational tractability. We prove that two commonly used approximation methods, the factorised Gaussian assumption and Monte Carlo dropout, lead to pathological estimates of the predictive uncertainty in single hidden layer ReLU networks. This indicates that more flexible approximations are needed to obtain reliable uncertainty estimates.

Rates of Convergence for Sparse Variational Gaussian Process Regression

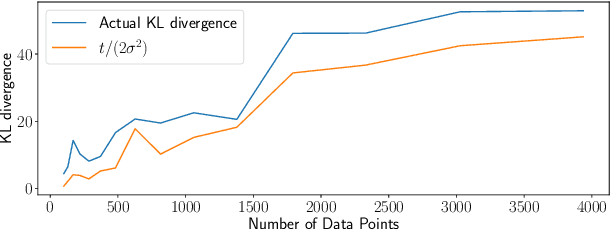
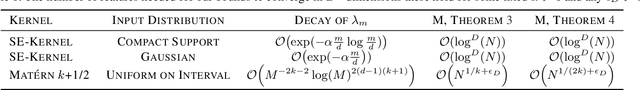
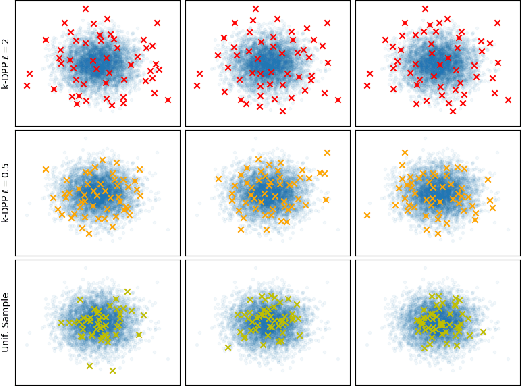
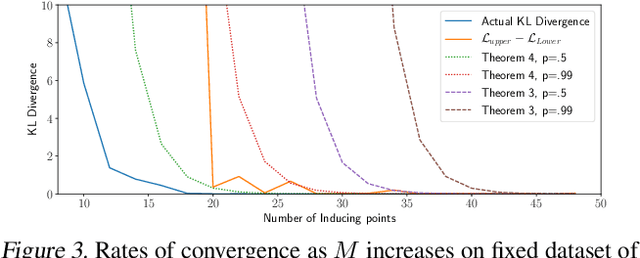
Excellent variational approximations to Gaussian process posteriors have been developed which avoid the $\mathcal{O}\left(N^3\right)$ scaling with dataset size $N$. They reduce the computational cost to $\mathcal{O}\left(NM^2\right)$, with $M\ll N$ being the number of inducing variables, which summarise the process. While the computational cost seems to be linear in $N$, the true complexity of the algorithm depends on how $M$ must increase to ensure a certain quality of approximation. We address this by characterising the behavior of an upper bound on the KL divergence to the posterior. We show that with high probability the KL divergence can be made arbitrarily small by growing $M$ more slowly than $N$. A particular case of interest is that for regression with normally distributed inputs in D-dimensions with the popular Squared Exponential kernel, $M=\mathcal{O}(\log^D N)$ is sufficient. Our results show that as datasets grow, Gaussian process posteriors can truly be approximated cheaply, and provide a concrete rule for how to increase $M$ in continual learning scenarios.