Causal Inference Using Tractable Circuits

The aim of this paper is to discuss a recent result which shows that probabilistic inference in the presence of (unknown) causal mechanisms can be tractable for models that have traditionally been viewed as intractable. This result was reported recently to facilitate model-based supervised learning but it can be interpreted in a causality context as follows. One can compile a non-parametric causal graph into an arithmetic circuit that supports inference in time linear in the circuit size. The circuit is also non-parametric so it can be used to estimate parameters from data and to further reason (in linear time) about the causal graph parametrized by these estimates. Moreover, the circuit size can sometimes be bounded even when the treewidth of the causal graph is not, leading to tractable inference on models that have been deemed intractable previously. This has been enabled by a new technique that can exploit causal mechanisms computationally but without needing to know their identities (the classical setup in causal inference). Our goal is to provide a causality-oriented exposure to these new results and to speculate on how they may potentially contribute to more scalable and versatile causal inference.

On Quantifying Literals in Boolean Logic and Its Applications to Explainable AI

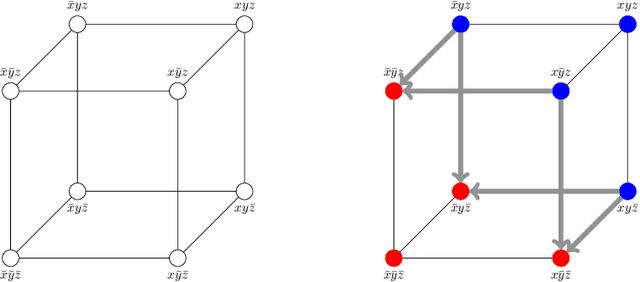
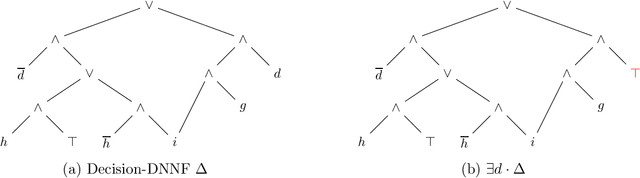
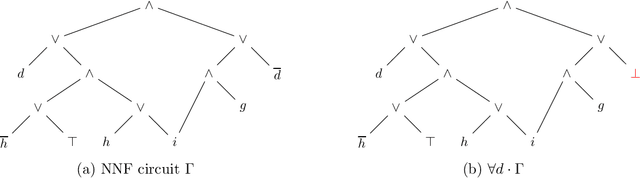
Quantified Boolean logic results from adding operators to Boolean logic for existentially and universally quantifying variables. This extends the reach of Boolean logic by enabling a variety of applications that have been explored over the decades. The existential quantification of literals (variable states) and its applications have also been studied in the literature. In this paper, we complement this by studying universal literal quantification and its applications, particularly to explainable AI. We also provide a novel semantics for quantification, discuss the interplay between variable/literal and existential/universal quantification. We further identify some classes of Boolean formulas and circuits on which quantification can be done efficiently. Literal quantification is more fine-grained than variable quantification as the latter can be defined in terms of the former. This leads to a refinement of quantified Boolean logic with literal quantification as its primitive.

On Symbolically Encoding the Behavior of Random Forests

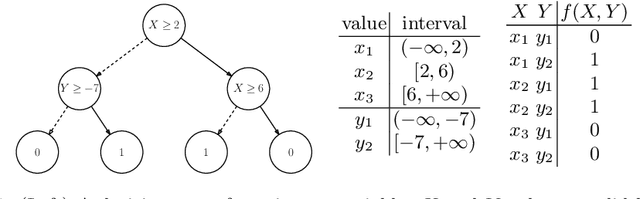
Recent work has shown that the input-output behavior of some machine learning systems can be captured symbolically using Boolean expressions or tractable Boolean circuits, which facilitates reasoning about the behavior of these systems. While most of the focus has been on systems with Boolean inputs and outputs, we address systems with discrete inputs and outputs, including ones with discretized continuous variables as in systems based on decision trees. We also focus on the suitability of encodings for computing prime implicants, which have recently played a central role in explaining the decisions of machine learning systems. We show some key distinctions with encodings for satisfiability, and propose an encoding that is sound and complete for the given task.

A New Perspective on Learning Context-Specific Independence

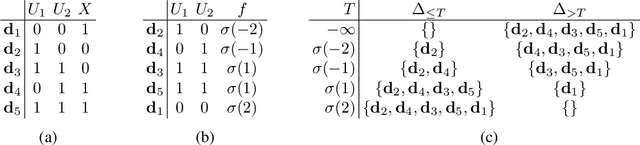
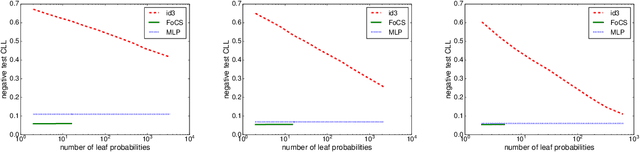
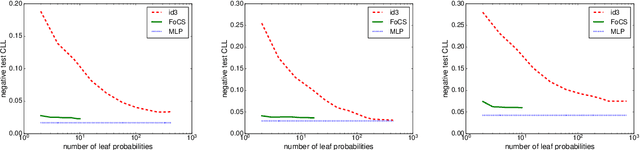
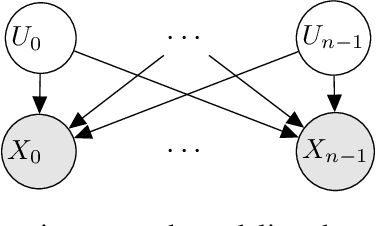
Local structure such as context-specific independence (CSI) has received much attention in the probabilistic graphical model (PGM) literature, as it facilitates the modeling of large complex systems, as well as for reasoning with them. In this paper, we provide a new perspective on how to learn CSIs from data. We propose to first learn a functional and parameterized representation of a conditional probability table (CPT), such as a neural network. Next, we quantize this continuous function, into an arithmetic circuit representation that facilitates efficient inference. In the first step, we can leverage the many powerful tools that have been developed in the machine learning literature. In the second step, we exploit more recently-developed analytic tools from explainable AI, for the purposes of learning CSIs. Finally, we contrast our approach, empirically and conceptually, with more traditional variable-splitting approaches, that search for CSIs more explicitly.

Three Modern Roles for Logic in AI

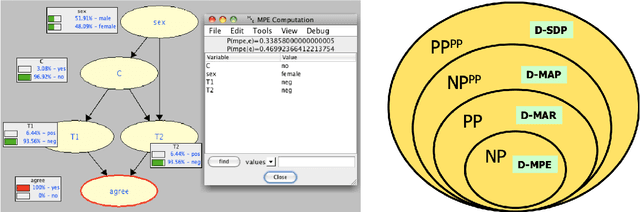
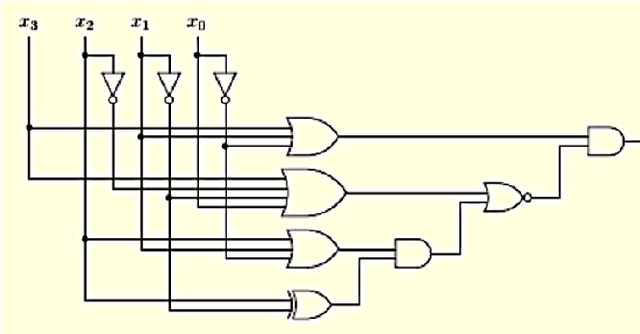
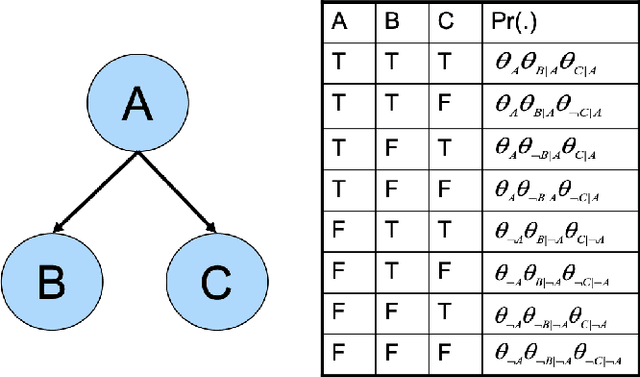
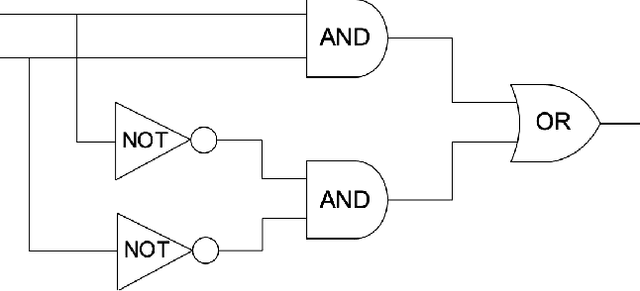
We consider three modern roles for logic in artificial intelligence, which are based on the theory of tractable Boolean circuits: (1) logic as a basis for computation, (2) logic for learning from a combination of data and knowledge, and (3) logic for reasoning about the behavior of machine learning systems.

On Tractable Representations of Binary Neural Networks

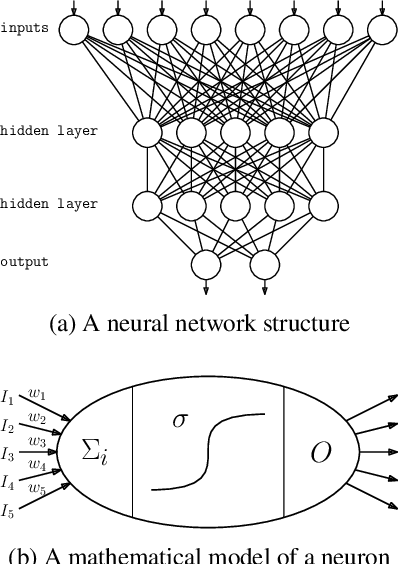
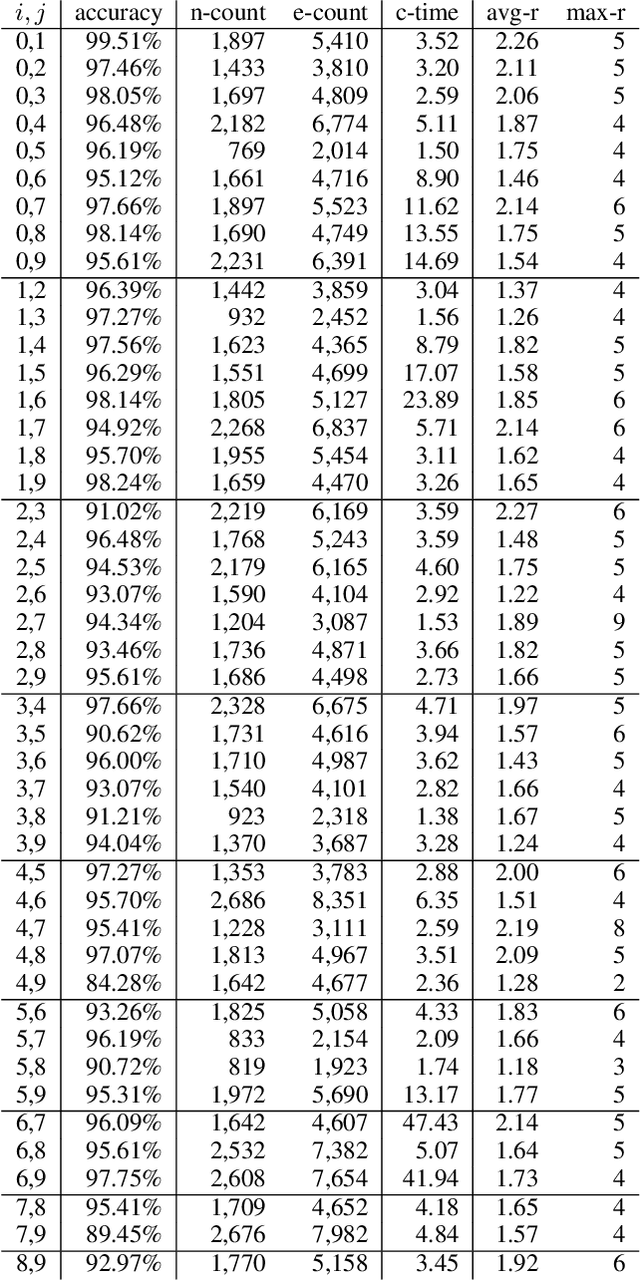
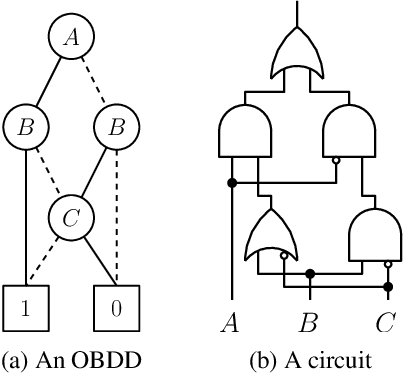
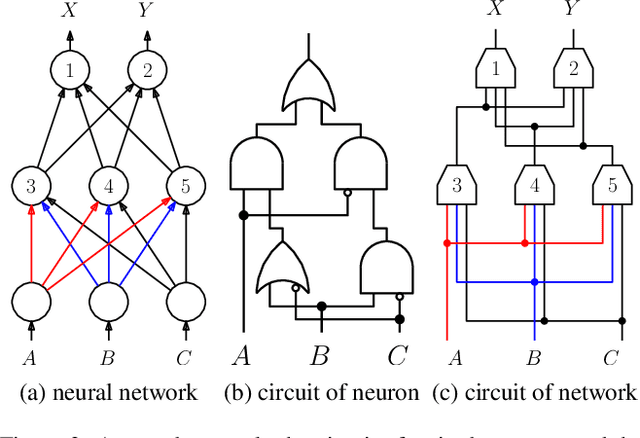
We consider the compilation of a binary neural network's decision function into tractable representations such as Ordered Binary Decision Diagrams (OBDDs) and Sentential Decision Diagrams (SDDs). Obtaining this function as an OBDD/SDD facilitates the explanation and formal verification of a neural network's behavior. First, we consider the task of verifying the robustness of a neural network, and show how we can compute the expected robustness of a neural network, given an OBDD/SDD representation of it. Next, we consider a more efficient approach for compiling neural networks, based on a pseudo-polynomial time algorithm for compiling a neuron. We then provide a case study in a handwritten digits dataset, highlighting how two neural networks trained from the same dataset can have very high accuracies, yet have very different levels of robustness. Finally, in experiments, we show that it is feasible to obtain compact representations of neural networks as SDDs.

An Advance on Variable Elimination with Applications to Tensor-Based Computation

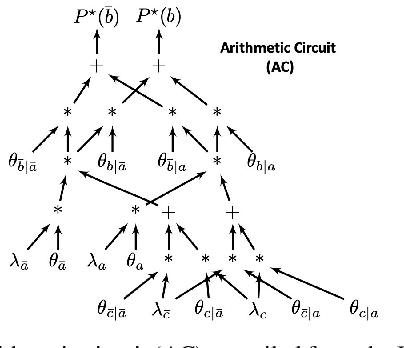
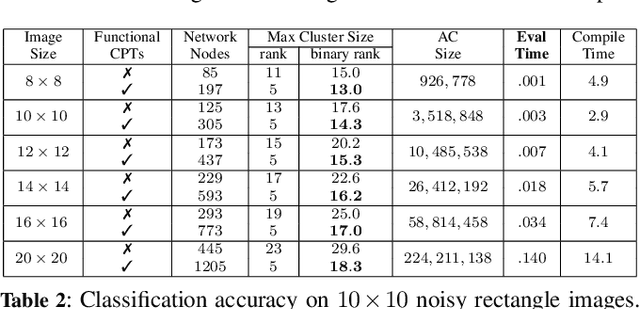
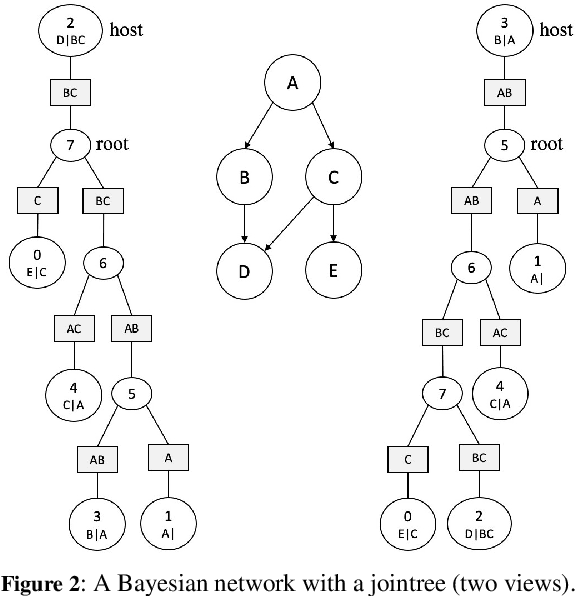
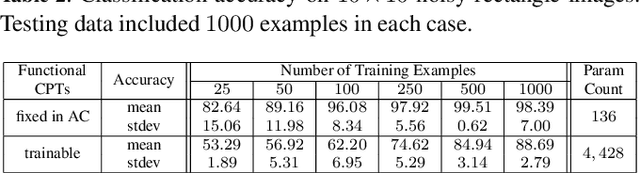
We present new results on the classical algorithm of variable elimination, which underlies many algorithms including for probabilistic inference. The results relate to exploiting functional dependencies, allowing one to perform inference and learning efficiently on models that have very large treewidth. The highlight of the advance is that it works with standard (dense) factors, without the need for sparse factors or techniques based on knowledge compilation that are commonly utilized. This is significant as it permits a direct implementation of the improved variable elimination algorithm using tensors and their operations, leading to extremely efficient implementations especially when learning model parameters. Moreover, the proposed technique does not require knowledge of the specific functional dependencies, only that they exist, so can be used when learning these dependencies. We illustrate the efficacy of our proposed algorithm by compiling Bayesian network queries into tensor graphs and then learning their parameters from labeled data using a standard tool for tensor computation.

On The Reasons Behind Decisions

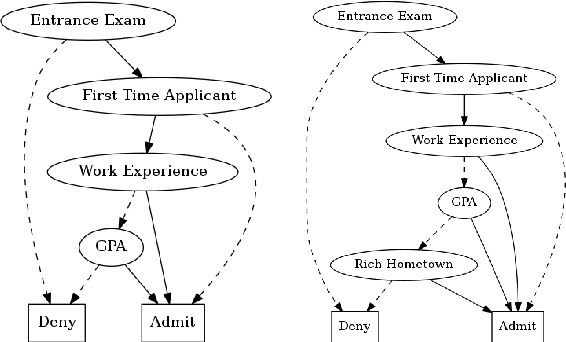
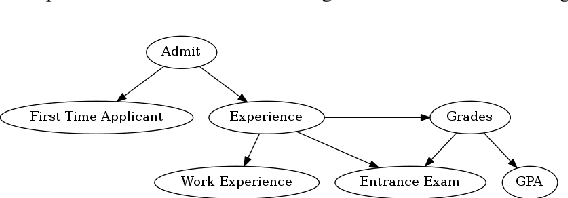
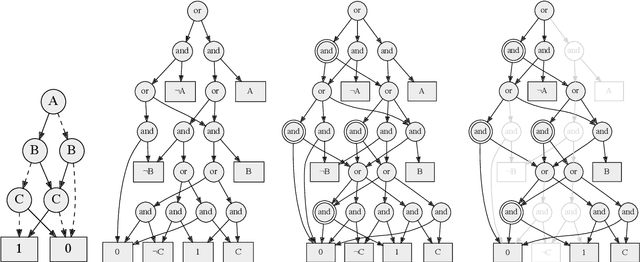
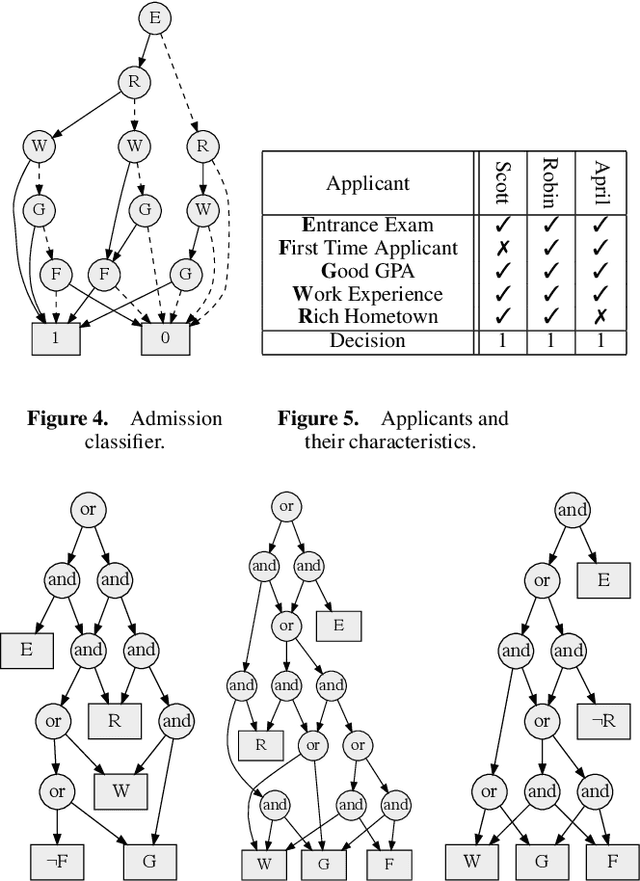
Recent work has shown that some common machine learning classifiers can be compiled into Boolean circuits that have the same input-output behavior. We present a theory for unveiling the reasons behind the decisions made by Boolean classifiers and study some of its theoretical and practical implications. We define notions such as sufficient, necessary and complete reasons behind decisions, in addition to classifier and decision bias. We show how these notions can be used to evaluate counterfactual statements such as "a decision will stick even if ... because ... ." We present efficient algorithms for computing these notions, which are based on new advances on tractable Boolean circuits, and illustrate them using a case study.

On the Relative Expressiveness of Bayesian and Neural Networks

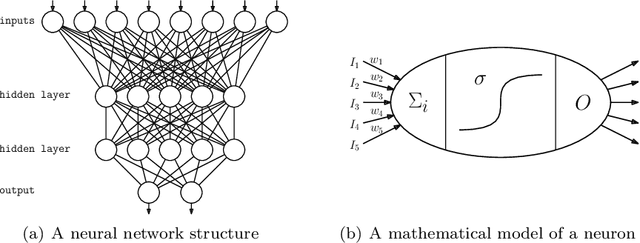
A neural network computes a function. A central property of neural networks is that they are "universal approximators:" for a given continuous function, there exists a neural network that can approximate it arbitrarily well, given enough neurons (and some additional assumptions). In contrast, a Bayesian network is a model, but each of its queries can be viewed as computing a function. In this paper, we identify some key distinctions between the functions computed by neural networks and those by marginal Bayesian network queries, showing that the former are more expressive than the latter. Moreover, we propose a simple augmentation to Bayesian networks (a testing operator), which enables their marginal queries to become "universal approximators."

A Symbolic Approach to Explaining Bayesian Network Classifiers

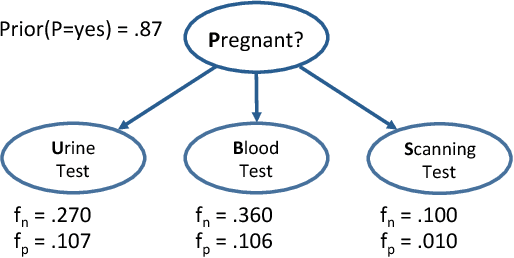
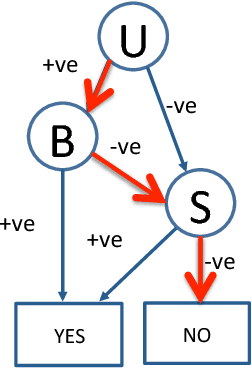
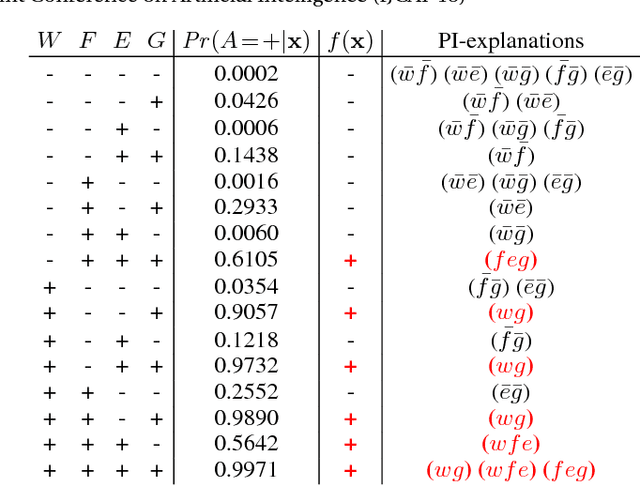
We propose an approach for explaining Bayesian network classifiers, which is based on compiling such classifiers into decision functions that have a tractable and symbolic form. We introduce two types of explanations for why a classifier may have classified an instance positively or negatively and suggest algorithms for computing these explanations. The first type of explanation identifies a minimal set of the currently active features that is responsible for the current classification, while the second type of explanation identifies a minimal set of features whose current state (active or not) is sufficient for the classification. We consider in particular the compilation of Naive and Latent-Tree Bayesian network classifiers into Ordered Decision Diagrams (ODDs), providing a context for evaluating our proposal using case studies and experiments based on classifiers from the literature.